Matemática Explorada

A princípio, na geometria plana, o conceito de área é fundamental para compreendermos a extensão de superfícies. Afinal, calcular áreas é essencial para resolver problemas práticos, além de ser uma base para outros estudos mais avançados da matemática. Nesse artigo, vamos explorar de forma didática e completa a área das principais figuras planas, além disso, você verá exemplos práticos, e diversos exercícios.

Desse modo, prepare-se para mergulhar neste tema e descobrir como calcular áreas de forma simples e eficiente!

O que é Área?

Em suma, a área de uma figura plana representa a medida da extensão de sua superfície. A área é expressa em unidades de medida quadradas, ou seja, centímetros quadrados (cm²), metros quadrados (m²), etc. Ou seja, ao calcular a área, estamos determinando quanto de espaço aquela figura ocupa em um plano. A fim de compreender melhor, imagine que você queira cobrir uma superfície com um determinado material, para saber quanto desse material você vai precisar, é preciso calcular a área.

Área das Principais Figuras Planas: Fórmulas e Exemplos

A seguir, vamos explorar as principais figuras planas e suas respectivas fórmulas para o cálculo da área:

• Quadrado:

  A área de um quadrado é calculada elevando-se a medida de um de seus lados ao quadrado. Dessa forma, se o lado do quadrado mede \(l\), a área \(A\) é:

  \( A = l^2 \)

  Exemplo: Se um quadrado possui lado de 5 cm, sua área é \(A = 5^2 = 25 cm^2\).

• Retângulo:

  A área de um retângulo é calculada multiplicando a medida da sua base pela medida da sua altura. Assim sendo, se a base do retângulo mede \(b\) e a altura mede \(h\), a área \(A\) é:

  \( A = b \times h \)

  Exemplo: Se um retângulo possui base de 8 cm e altura de 4 cm, sua área é \(A = 8 \times 4 = 32 cm^2\).

• Triângulo:

  A área de um triângulo é calculada multiplicando a medida da sua base pela medida da sua altura e dividindo o resultado por dois. A saber, se a base do triângulo mede \(b\) e a altura mede \(h\), a área \(A\) é:

  \( A = \frac{b \times h}{2} \)

  Exemplo: Se um triângulo possui base de 10 cm e altura de 6 cm, sua área é \(A = \frac{10 \times 6}{2} = 30 cm^2\).

• Paralelogramo:

  A área de um paralelogramo é calculada multiplicando a medida da sua base pela medida da sua altura. Similarmente, se a base do paralelogramo mede \(b\) e a altura mede \(h\), a área \(A\) é:

  \( A = b \times h \)

  Exemplo: Se um paralelogramo possui base de 12 cm e altura de 5 cm, sua área é \(A = 12 \times 5 = 60 cm^2\).

• Trapézio:

  A área de um trapézio é calculada somando as medidas das bases, multiplicando o resultado pela medida da altura e dividindo tudo por 2. Portanto, se a base maior do trapézio mede \(B\), a base menor mede \(b\) e a altura mede \(h\), a área \(A\) é:

  \( A = \frac{(B + b) \times h}{2} \)

  Exemplo: Se um trapézio possui base maior de 10 cm, base menor de 6 cm e altura de 4 cm, sua área é \(A = \frac{(10 + 6) \times 4}{2} = 32 cm^2\).

• Círculo:

  A área de um círculo é calculada multiplicando a constante \(\pi\) pelo quadrado da medida do seu raio. Ou seja, se o raio do círculo mede \(r\), a área \(A\) é:

  \( A = \pi \times r^2 \)

  Exemplo: Se um círculo possui raio de 7 cm, sua área é \(A = \pi \times 7^2 = 49\pi cm^2\).

• Losango:

  A área de um losango é calculada multiplicando as medidas das suas diagonais e dividindo o resultado por 2. Assim, se a diagonal maior do losango mede \(D\) e a diagonal menor mede \(d\), a área \(A\) é:

  \( A = \frac{D \times d}{2} \)

  Exemplo: Se um losango possui diagonal maior de 12 cm e diagonal menor de 8 cm, sua área é \(A = \frac{12 \times 8}{2} = 48 cm^2\).

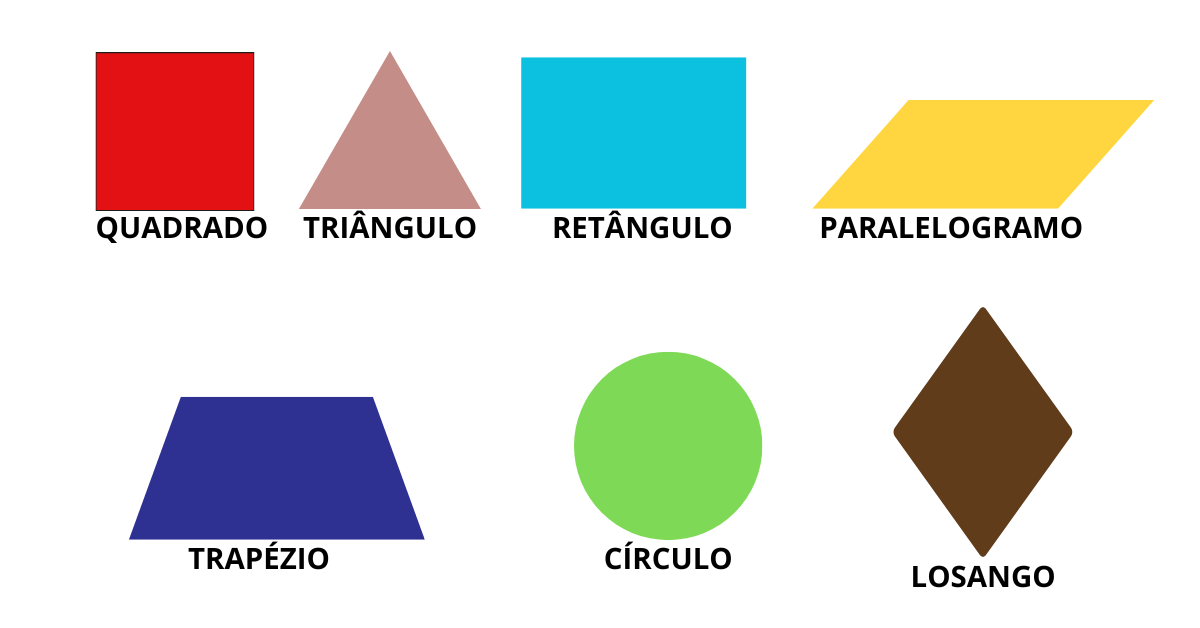
A saber, cada uma dessas figuras possui suas particularidades, e a aplicação correta da fórmula é essencial para obter o resultado correto. Por isso, continue estudando para solidificar seu aprendizado.

Importância do Cálculo de Áreas

O cálculo de áreas é, por certo, um conceito fundamental em diversas áreas do conhecimento e em situações cotidianas. Desde o planejamento de construções e design de objetos até o cálculo de áreas em mapas e terrenos, este conhecimento é, sem dúvida, indispensável.

Em suma, o estudo da área de figuras planas é um tema recorrente em provas de concursos e vestibulares, principalmente quando se trata de matemática e física. Afinal, muitas situações problemas utilizam o conceito de área como base para a sua resolução.

Exercícios Resolvidos

A fim de solidificar o que aprendemos até agora, vamos resolver alguns exercícios juntos. Preste bastante atenção e tente entender cada etapa!

Exercícios Propostos: Desafie-se!

Agora, chegou a sua vez! Resolva os exercícios abaixo e, em seguida, compare suas respostas com a resolução passo a passo. Lembre-se, o mais importante é tentar e aprender com seus erros!

Se, porventura, você queira explorar mais este tema, não deixe de conferir este vídeo incrível do nosso canal: Vídeos sobre Geometria no Matemática Explorada, onde explicamos em detalhes vários assuntos sobre geometria. Similarmente, você também pode explorar outros assuntos relacionados como poliedros aqui no nosso site.

Conclusão

Finalmente, o cálculo da área de figuras planas é uma ferramenta essencial para muitos aspectos da matemática e também para diversas situações práticas no nosso cotidiano. Assim sendo, dominar as fórmulas e entender como calcular a área de cada figura é um conhecimento muito útil. Ou seja, continue estudando e explorando os fascinantes mistérios da matemática! Compartilhe este artigo com seus amigos e deixe seu comentário abaixo!