Matemática Explorada

Primordialmente, em nosso artigo anterior, Funções: O Que São e Como Surgem as Relações Matemáticas, exploramos a essência das funções e suas origens. Agora, neste novo artigo, vamos nos aprofundar em como podemos representar essas relações matemáticas, utilizando diferentes ferramentas como diagramas de flechas, pares ordenados, expressões algébricas e gráficos. Assim sendo, prepare-se para desvendar as diversas formas de visualizar e entender as funções!

Sobretudo, a representação de funções é crucial para compreender como elas funcionam e como podemos aplicá-las em diversos contextos. Inegavelmente, cada método de representação oferece uma perspectiva única e valiosa, que nos permite analisar e interpretar as relações matemáticas de maneira mais eficaz. Portanto, vamos explorar cada uma dessas representações e ver como elas se conectam.

Representação de Funções

Diagrama de Flechas

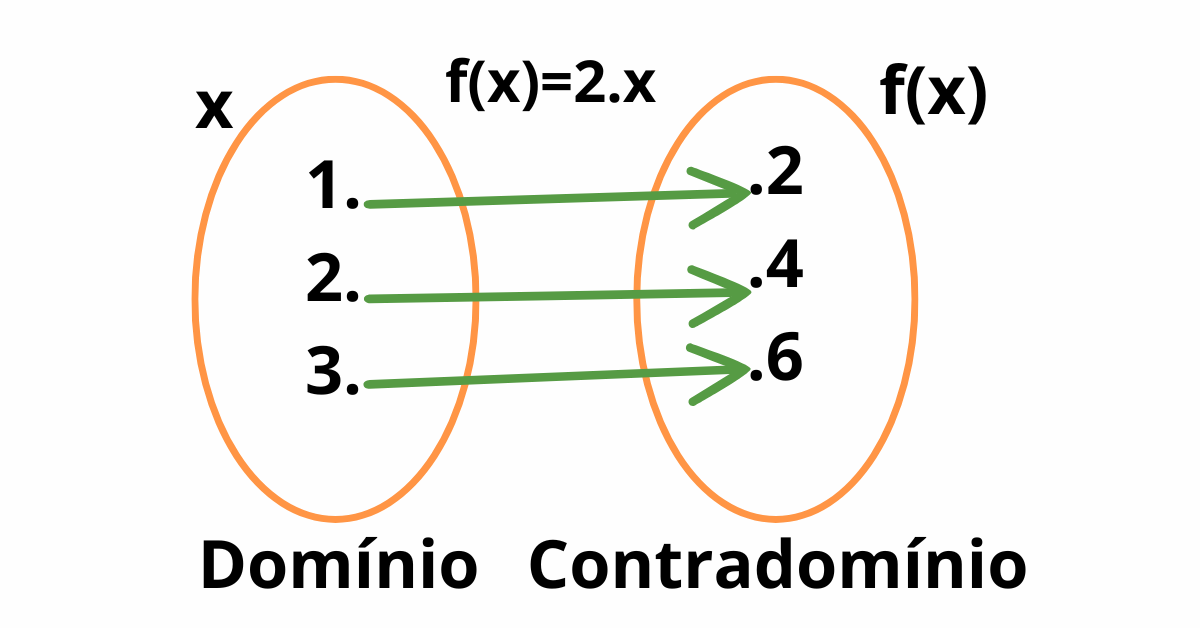
Anteriormente, introduzimos o diagrama de flechas como uma forma de representar relações entre conjuntos. Analogamente, no contexto das funções, o diagrama de flechas ilustra claramente como cada elemento do domínio (conjunto de partida) é associado a um único elemento do contradomínio (conjunto de chegada). Por exemplo, considere a função f que associa cada número ao seu dobro. O diagrama de flechas mostraria setas saindo de cada número do domínio para seu dobro no contradomínio.

Pares Ordenados

Além disso, podemos representar funções por meio de pares ordenados. Em resumo, um par ordenado (x, y) indica que o elemento x do domínio está associado ao elemento y do contradomínio através da função. Nesse sentido, cada par ordenado corresponde a uma “seta” no diagrama de flechas.

Expressões Algébricas

De fato, uma das formas mais comuns de representar funções é através de expressões algébricas. Isto é, essas expressões definem a relação entre os elementos do domínio e do contradomínio por meio de fórmulas matemáticas. Assim sendo, com uma expressão algébrica, podemos calcular a imagem de qualquer elemento do domínio.

Gráficos (Introdução)

Ademais, as funções podem ser visualizadas graficamente em um plano cartesiano. Nesse ínterim, cada par ordenado (x, y) é representado por um ponto no gráfico. Assim, ao ligar esses pontos, podemos obter uma representação visual da função, que nos permite entender seu comportamento de forma intuitiva.

Só para ilustrar, um gráfico mostra como a variável y (imagem) varia em função da variável x (domínio), facilitando a análise do crescimento ou decrescimento da função. Mais adiante, exploraremos os gráficos com mais detalhes.

Notação de Funções

Principalmente, a notação de funções é essencial para expressar matematicamente as relações. Em resumo, usamos a notação f(x) para indicar a imagem de x pela função f. Em outras palavras, f(x) é o valor que a função f atribui ao elemento x.

Assim também, a notação f(x) = y indica que a imagem de x pela função f é y. Logo, f(x) representa o valor que obtemos quando aplicamos a função f ao valor x, que é igual ao valor y.

Além disso, é crucial entender os termos:

• Domínio: É o conjunto de todos os valores de entrada (x) para os quais a função está definida.
• Contradomínio: É o conjunto que contém todos os possíveis valores de saída (y) da função.
• Imagem: É o conjunto de todos os valores de saída (y) que são efetivamente obtidos quando aplicamos a função aos valores do domínio. A imagem é um subconjunto do contradomínio.

Encontrando Imagens

Atualmente, para encontrar a imagem de um valor específico, basta substituir esse valor na expressão algébrica da função. Por exemplo, se temos a função \( f(x) = x + 1 \) e queremos encontrar a imagem de x = 3, basta calcular \( f(3) = 3 + 1 = 4 \). Portanto, a imagem de 3 pela função f é 4.

Nesse sentido, o processo de encontrar imagens se conecta diretamente com as outras formas de representação. Isto é, no diagrama de flechas, estaríamos seguindo a seta que sai do 3 até o 4; nos pares ordenados, teríamos o par (3, 4), e no gráfico, o ponto (3, 4).

Onde as Funções Aparecem

Conforme vimos anteriormente, as funções estão presentes em diversas situações do nosso dia a dia. Por exemplo, a relação entre o tempo e a distância percorrida por um carro pode ser descrita por uma função. Similarmente, a relação entre o preço e a quantidade de um produto também pode ser modelada por uma função.

Além disso, as funções são ferramentas essenciais em áreas como a física, onde modelam fenômenos como a trajetória de um projétil; na economia, onde são usadas para analisar o crescimento de uma empresa; e em muitas outras áreas da ciência e tecnologia. De fato, entender as funções é fundamental para compreender o mundo que nos cerca.

Importância e Conexão com Próximos Artigos

Em conclusão, as funções são um conceito fundamental na matemática e em suas aplicações práticas. Acima de tudo, dominar as diferentes formas de representar as funções é crucial para avançar nos estudos matemáticos. Todavia, este é apenas o começo de nossa jornada de exploração do mundo das funções.

Nesse sentido, nos próximos artigos, exploraremos os diferentes tipos de funções, como funções lineares, quadráticas e exponenciais, além de nos aprofundarmos na representação gráfica das funções. A saber, prepare-se para continuar sua jornada de aprendizado conosco!

Para complementar seus estudos, você pode conferir nossos artigos sobre Funções: O Que São e Como Surgem as Relações Matemáticas e Retas Perpendiculares, onde você poderá explorar mais sobre geometria!

Não perca a oportunidade de aprender mais! Inscreva-se agora em nosso canal no YouTube e descubra vídeos incríveis sobre matemática: Matemática Explorada. **Junte-se à nossa comunidade e vamos desvendar os mistérios da matemática juntos!**

Exercícios Propostos