Matemática Explorada

A princípio, na geometria plana, a circunferência é uma figura fundamental que aparece em inúmeras situações cotidianas, e um dos conceitos mais importantes relacionados a essa figura é o seu comprimento. Afinal, compreender como determinar essa medida é essencial para uma variedade de aplicações e para o estudo da geometria e da matemática em geral. Neste artigo, vamos explorar esses conceitos em detalhes, incluindo definições, exemplos práticos e exercícios para fixação do conteúdo.

Dessa forma, prepare-se para explorar a matemática de forma didática e clara, em outras palavras, como um verdadeiro livro didático, onde cada etapa é explicada de forma simples, e também apresentando uma visão geral sobre a circunferência e a importância de seus elementos.

Definindo a Circunferência e Seus Elementos Essenciais

A princípio, uma circunferência é definida como o conjunto de todos os pontos em um plano que estão a uma mesma distância de um ponto fixo, chamado de centro. Assim sendo, é importante você entender os principais elementos de uma circunferência:

• Raio: A distância entre o centro da circunferência e qualquer ponto da sua borda.
• Diâmetro: Qualquer segmento de reta que passa pelo centro da circunferência e une dois pontos opostos de sua borda. É o dobro do raio.
• Centro: Ponto equidistante de todos os pontos da circunferência.

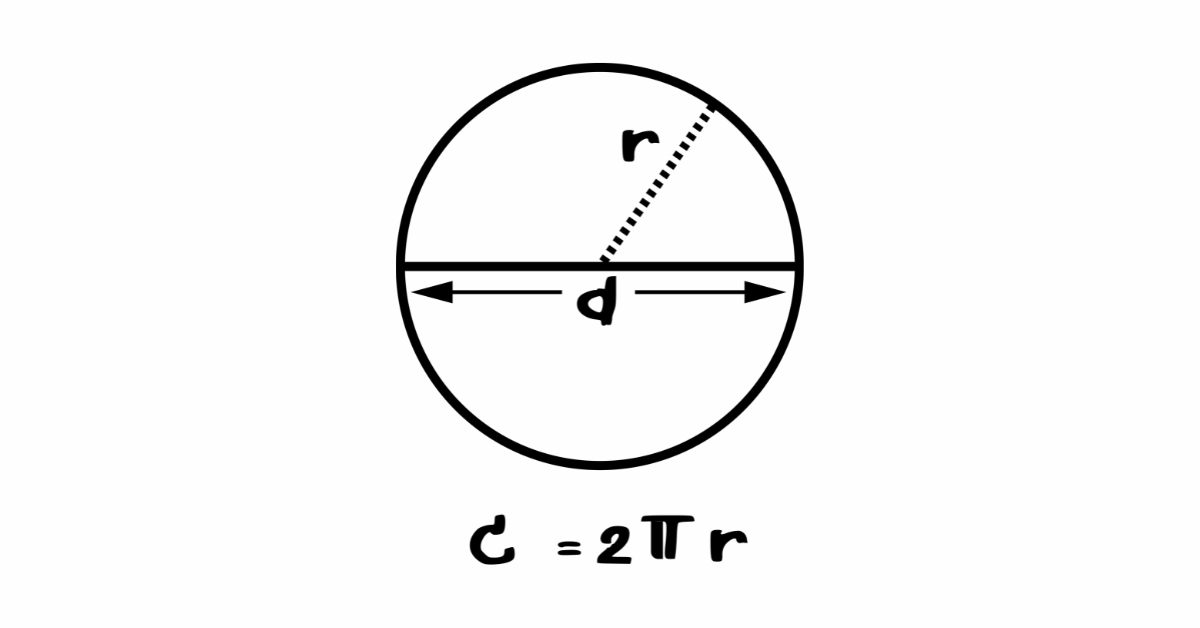
Representação gráfica de uma circunferência e seus elementos.

Descobrindo a Fórmula da Extensão da Circunferência

Para calcular a extensão de uma circunferência, usamos a seguinte fórmula:

\(C = 2 \pi r\) ou \(C = \pi d\)

Onde:

• \(C\) é o comprimento da circunferência.
• \(\pi\) (pi) é uma constante irracional aproximadamente igual a 3,14159.
• \(r\) é o raio da circunferência.
• \(d\) é o diâmetro da circunferência (sendo que \(d = 2r\)).

Em suma, a fórmula mostra que a medida da circunferência é diretamente proporcional ao seu raio (ou diâmetro) e também depende do número \(\pi\).

O Número Pi (π): Um Número Misterioso

O número \(\pi\), é, sem dúvida, uma das constantes mais importantes da matemática e, por conseguinte, aparece em muitos cálculos envolvendo circunferências e círculos. Aliás, esse número é irracional, o que significa que ele possui infinitas casas decimais não periódicas. A saber, suas primeiras casas decimais são 3,14159, e esse número tem uma história muito rica e complexa.

Similarmente, o estudo do número pi, remonta aos matemáticos da antiguidade. Arquimedes, um matemático grego que viveu no século III a.C, já se dedicava a calcular uma aproximação para o número pi, usando polígonos inscritos e circunscritos em uma circunferência. Portanto, ao longo dos séculos, diversos matemáticos contribuíram para nosso conhecimento do número \(\pi\), e suas propriedades.

Aplicações Práticas da Medida da Circunferência

Decerto, a extensão de uma circunferência não é apenas um conceito abstrato da matemática. Afinal, ele aparece em muitas situações práticas do dia a dia. Veja alguns exemplos:

• Rodas: A medida da circunferência de uma roda define a distância percorrida a cada volta.
• Embalagens: O comprimento da circunferência é usado para criar embalagens cilíndricas de diversos produtos.
• Pistas de Corrida: Para projetar pistas de atletismo, é fundamental calcular o comprimento das curvas.
• Engrenagens: Em máquinas e equipamentos, a medida da circunferência das engrenagens define o movimento e a transmissão de força.
• Design de Objetos: Designers utilizam o comprimento da circunferência para criar objetos com forma circular, tais como vasos, anéis, etc.

Como resultado, o entendimento do comprimento da circunferência não apenas nos auxilia nos estudos, mas também nos permite compreender e resolver problemas do mundo real.

Exercícios Resolvidos: Passo a Passo

A fim de consolidar o que aprendemos até agora, vamos resolver alguns exercícios juntos. Preste bastante atenção e tente entender cada etapa!

Exercícios Propostos: Teste seus conhecimentos!

Agora, chegou a sua vez! Resolva os exercícios abaixo e, em seguida, compare suas respostas com a resolução passo a passo. Lembre-se, o mais importante é tentar e aprender com seus erros!