Na vasta área da geometria analítica, um dos conceitos mais básicos e, simultaneamente, essenciais, é o cálculo da distância entre dois pontos. Afinal, compreender como determinar essa distância é fundamental para o estudo de diversas figuras geométricas e para a resolução de problemas práticos e teóricos. Neste artigo, vamos explorar, em detalhes, a fórmula da distância entre dois pontos; você verá exemplos práticos, aplicações no cotidiano e, por fim, exercícios para você praticar.
Assim, a distância entre dois pontos é uma medida que indica o quão afastados esses pontos estão em um plano ou espaço. Decerto, essa medida pode ser calculada utilizando-se diversas ferramentas matemáticas e, por conseguinte, essa medida é expressa em unidades de comprimento, como centímetros, metros, quilômetros, etc.
A Importância Histórica da Fórmula da Distância
A geometria, anteriormente, já era uma área de grande interesse e estudo, e a necessidade de calcular distâncias era essencial para construções, cartografia e navegação. Com o desenvolvimento da geometria analítica, essa relação se tornou mais precisa e, atualmente, é indispensável para diversas áreas, como a física, a computação e a engenharia. Matemáticos como René Descartes, com a criação do plano cartesiano, abriram caminho para a formalização da fórmula da distância, permitindo cálculos mais eficientes e precisos.
Sobretudo, esses estudos nos permitiram entender melhor o mundo que nos cerca e desenvolver tecnologias que utilizamos hoje, como a arquitetura e a engenharia. Todavia, entender a fórmula da distância não é apenas uma questão de memorização, mas também uma oportunidade de explorar a história da matemática e seus avanços.
O Conceito da Distância entre Dois Pontos
Em suma, a distância entre dois pontos é a medida do menor segmento de reta que une esses pontos. Para facilitar a compreensão, vamos analisar esse conceito em um plano cartesiano:
Suponha que temos dois pontos, \(A(x_1, y_1)\) e \(B(x_2, y_2)\), em um plano cartesiano. A distância entre esses dois pontos, que chamaremos de \(d_{AB}\), é dada pela seguinte fórmula:
\(d_{AB} = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}\)
Nesse sentido, essa fórmula é conhecida como a fórmula da distância euclidiana, e é, de fato, uma das ferramentas mais utilizadas na geometria analítica.
Como Calcular a Distância Entre Dois Pontos
Assim sendo, o cálculo da distância entre dois pontos envolve alguns passos simples:
- Identifique as coordenadas dos dois pontos.
- Subtraia as coordenadas x e eleve ao quadrado.
- Subtraia as coordenadas y e eleve ao quadrado.
- Some os resultados das etapas anteriores.
- Calcule a raiz quadrada da soma.
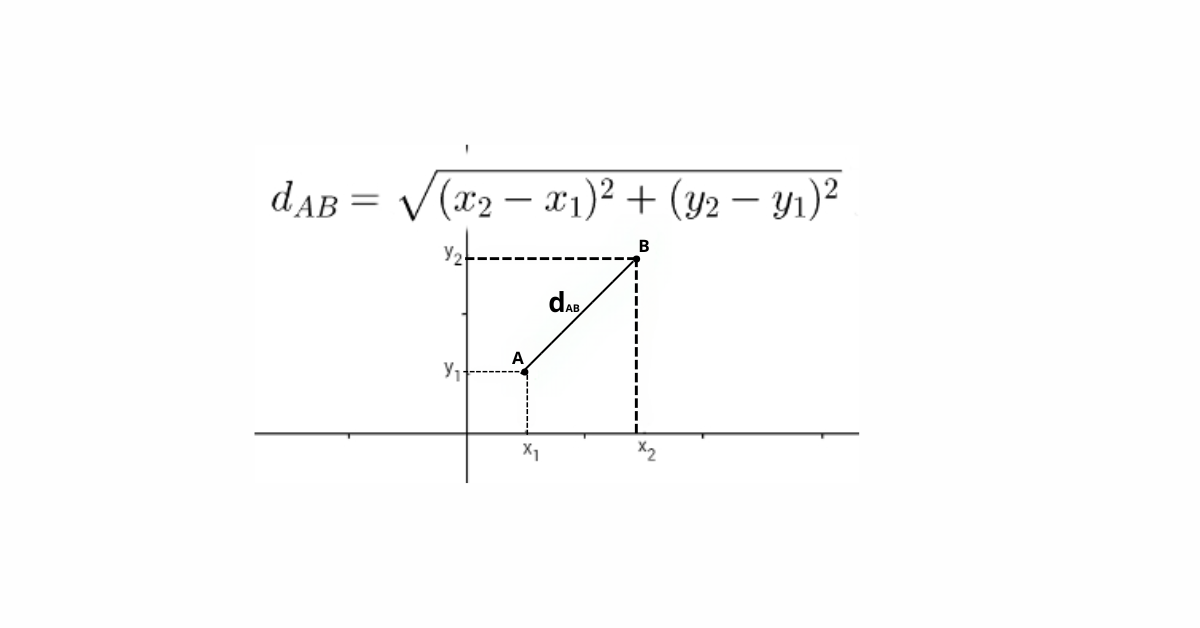
Representação da distância entre dois pontos em um plano cartesiano.
Exemplos Práticos do Cálculo da Distância
Para entender melhor o conceito, observe, por exemplo, alguns exemplos práticos:
Exemplo 1
Calcule a distância entre os pontos \(A(1, 2)\) e \(B(4, 6)\).
Utilizando a fórmula, temos:
\(d_{AB} = \sqrt{(4 – 1)^2 + (6 – 2)^2}\)
\(d_{AB} = \sqrt{3^2 + 4^2}\)
\(d_{AB} = \sqrt{9 + 16}\)
\(d_{AB} = \sqrt{25}\)
\(d_{AB} = 5\)
Portanto, a distância entre os pontos \(A\) e \(B\) é de 5 unidades de comprimento.
Exemplo 2
Calcule a distância entre os pontos \(C(-2, 3)\) e \(D(3, -1)\).
Aplicando a fórmula:
\(d_{CD} = \sqrt{(3 – (-2))^2 + (-1 – 3)^2}\)
\(d_{CD} = \sqrt{5^2 + (-4)^2}\)
\(d_{CD} = \sqrt{25 + 16}\)
\(d_{CD} = \sqrt{41}\)
Assim, a distância entre os pontos \(C\) e \(D\) é de \(\sqrt{41}\) unidades de comprimento.
Aplicações da Distância entre Dois Pontos no Cotidiano
Eventualmente, você pode se perguntar onde este conceito é aplicado no nosso dia a dia? Observe, por exemplo, alguns exemplos:
- GPS: Sistemas de GPS usam a fórmula da distância para calcular rotas e indicar a sua localização exata.
- Games: Em jogos de computador, a distância entre personagens e objetos é calculada para determinar interações e movimentos.
- Engenharia: Engenheiros utilizam este conceito para planejar construções, rotas de transporte e projetos de infraestrutura.
- Cartografia: A distância entre dois pontos é fundamental para a criação e leitura de mapas.
- Robótica: A robótica utiliza esse conceito para programar movimentos e a interação dos robôs em um espaço físico.
Distância entre Dois Pontos e Outros Conceitos Matemáticos
Finalmente, para uma compreensão completa do assunto, é preciso que você saiba como a distância entre dois pontos está relacionada com outros conceitos matemáticos: Inegavelmente, a distância entre dois pontos é um dos conceitos mais importantes na matemática, e está presente em diversos outros conceitos. Principalmente para entender o conceito de módulo de um vetor.
- Teorema de Pitágoras: O cálculo da distância entre dois pontos em um plano cartesiano é, sem dúvida, uma aplicação do teorema de Pitágoras.
- Geometria Analítica: A distância entre dois pontos é fundamental para o estudo da geometria analítica, que combina álgebra e geometria para analisar figuras geométricas.
- Vetores: O conceito de distância é intimamente relacionado aos vetores, que são usados para representar deslocamentos e forças no espaço.
Exercícios Resolvidos
A fim de solidificar o que aprendemos até agora, vamos resolver alguns exercícios juntos. Preste bastante atenção e tente entender cada etapa!
Exercício 1
Duas retas, \(r\) e \(s\), se cruzam em um ponto. Se o ângulo formado por elas for de 90 graus, o que podemos afirmar sobre \(r\) e \(s\)?
Resolução:
Se o ângulo formado entre \(r\) e \(s\) é de 90 graus, então, por definição, as retas são perpendiculares.
Portanto, \(r \perp s\)
Exercício 2
Em um plano cartesiano, a reta \(t\) tem coeficiente angular igual a 2. Qual deve ser o coeficiente angular de uma reta \(u\) para que ela seja perpendicular a \(t\)?
Resolução:
Para que duas retas sejam perpendiculares, o produto de seus coeficientes angulares deve ser igual a -1. Seja \(m_t\) o coeficiente angular da reta \(t\) e \(m_u\) o coeficiente angular da reta \(u\). Temos que \(m_t = 2\). Então:
\(m_t \cdot m_u = -1\)
\(2 \cdot m_u = -1\)
\(m_u = – \frac{1}{2}\)
Assim, o coeficiente angular de \(u\) deve ser \(-\frac{1}{2}\).
Exercício 3
Um triângulo tem um ângulo de 90 graus. O que podemos afirmar sobre este triângulo?
Resolução:
Um triângulo com um ângulo de 90 graus é chamado de triângulo retângulo. Os dois lados que formam esse ângulo são perpendiculares entre si.
Exercícios Propostos
Agora, chegou a sua vez! Resolva os exercícios abaixo e, em seguida, compare suas respostas com a resolução passo a passo. Lembre-se, o mais importante é tentar e aprender com seus erros!
Exercício 4
Qual a distância entre os pontos \(A(1, 1)\) e \(B(5, 4)\)?
Exercício 5
Qual a distância entre os pontos \(P(-2, 1)\) e \(Q(2, -2)\)?
Exercício 6
Qual a distância entre os pontos \(R(0, 0)\) e \(S(8, 6)\)?
Exercício 7
Qual a distância entre os pontos \(M(-3, -2)\) e \(N(1, 1)\)?
Exercício 8
Se um ponto está na origem \((0,0)\) e outro está em \((5, 12)\), qual é a distância entre eles?
Exercício 9
Qual a distância entre os pontos \(A(-1, 2)\) e \(B(3, 5)\)?
Se, porventura, você queira explorar mais este tema, não deixe de conferir este vídeo incrível do nosso canal: Vídeos sobre Geometria no Matemática Explorada, onde explicamos em detalhes vários assuntos sobre geometria. Similarmente, você também pode explorar outros assuntos relacionados como retas perpendiculares aqui no nosso site.
Conclusão
Finalmente, o estudo da distância entre dois pontos é, sem dúvida, indispensável para a compreensão da geometria analítica e suas aplicações. Afinal, com a fórmula da distância, você pode calcular a distância entre quaisquer dois pontos no plano cartesiano, e usar esse conceito para diversas áreas. Ou seja, o seu aprendizado não deve parar por aqui. Portanto, continue estudando e explorando os fascinantes mistérios da matemática.

Deixe um comentário