**Anteriormente**, exploramos as funções modulares e suas aplicações, **conforme** você pode conferir no artigo Função Modular: Definição, Gráfico e Aplicações Práticas. **Agora**, vamos estudar uma classe de funções muito importante: as funções exponenciais. **Afinal**, elas estão presentes em diversos fenômenos do nosso cotidiano, desde o crescimento de populações até o decaimento radioativo.
**Assim**, entender as funções exponenciais é fundamental para compreendermos o mundo ao nosso redor. **Dessa forma**, vamos explorar suas características, propriedades e aplicações.
Definição Formal da Função Exponencial
**Primeiramente**, a função exponencial é definida pela seguinte lei de formação:
\(f(x) = a^x\)
Nessa expressão, \(a\) é uma constante real, denominada base, que deve ser maior que zero e diferente de 1 \( (a > 0 \text{ e } a \neq 1) \) . O expoente \(x\) é a variável independente, que pode assumir qualquer valor real.
**Em outras palavras**, a função exponencial associa um número real \(x\) a um valor que é obtido elevando a base \(a\) a esse expoente. **Por exemplo**, se \(a = 2\), temos a função \(f(x) = 2^x\).
**Ademais**, existe uma base especial para funções exponenciais, que é o número de Euler, representado pela letra \(e\). O valor de \(e\) é aproximadamente 2,71828. **Portanto**, uma função exponencial com essa base é escrita como \(f(x) = e^x\), e também é de grande importância na matemática e em diversas áreas da ciência.
Gráfico da Função Exponencial
**Certamente**, o gráfico da função exponencial tem características particulares que o diferenciam de outros tipos de funções. **Aliás**, a forma do gráfico depende do valor da base \(a\).
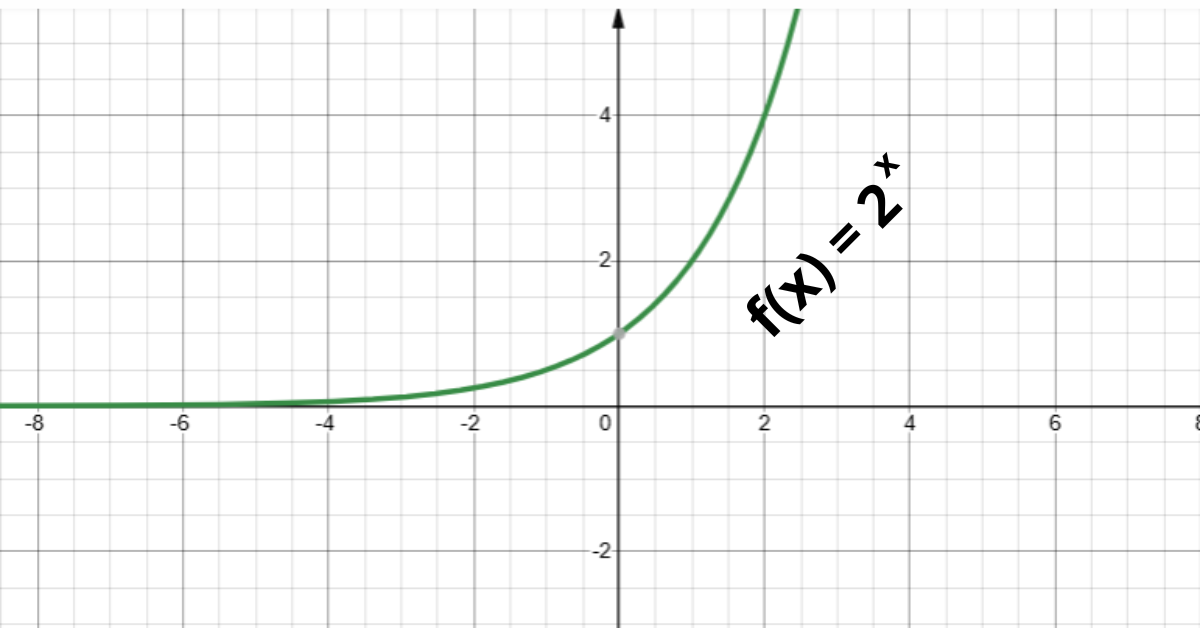
**Em geral**, se \(a > 1\), a função exponencial é crescente, ou seja, à medida que o valor de \(x\) aumenta, o valor de \(f(x)\) também aumenta. **Nesse sentido**, o gráfico se eleva da esquerda para a direita.
**Por outro lado**, se \(0 < a < 1\), a função exponencial é decrescente, ou seja, à medida que o valor de \(x\) aumenta, o valor de \(f(x)\) diminui. **Portanto**, o gráfico cai da esquerda para a direita.
**Em virtude disso**, o gráfico da função exponencial sempre passa pelo ponto \((0,1)\), pois \(a^0 = 1\) para qualquer base \(a\) (exceto 0). **Além disso**, o eixo x é uma assíntota horizontal, o que significa que o gráfico se aproxima do eixo x, mas nunca o toca.
Propriedades da Função Exponencial
**Similarmente** a outras funções, as funções exponenciais possuem algumas propriedades importantes que nos ajudam a entender seu comportamento e a resolver problemas. **Assim**, algumas delas são:
- \(a^x \cdot a^y = a^{x+y}\): Multiplicação de potências de mesma base.
- \(\frac{a^x}{a^y} = a^{x-y}\): Divisão de potências de mesma base.
- \((a^x)^y = a^{xy}\): Potência de potência.
- \(a^0 = 1\): Qualquer número (diferente de zero) elevado a zero é igual a 1.
- \(a^1 = a\): Qualquer número elevado a 1 é igual a ele mesmo.
- \((ab)^x = a^x \cdot b^x\): Potência de um produto
- \(\left(\frac{a}{b}\right)^x = \frac{a^x}{b^x}\): Potência de uma divisão
Equações Exponenciais
**Logo**, uma equação exponencial é aquela que possui a incógnita no expoente. **Afinal**, para resolver essas equações, geralmente buscamos igualar as bases para, então, igualar os expoentes.
**Contudo**, nem sempre é possível igualar as bases diretamente, e nesses casos, podemos usar a propriedade dos logaritmos (que veremos em um artigo futuro) para resolver.
**Por exemplo**, vamos resolver a equação \( 2^x = 8 \):
**Primeiramente**, reescrevemos o número 8 como uma potência de base 2: \( 2^x = 2^3 \).
**Em seguida**, como as bases são iguais, podemos igualar os expoentes: \( x = 3 \).
**Dessa forma**, a solução da equação é \(x = 3\).
**Analogamente**, vamos resolver a equação \( 3^x = \frac{1}{27} \)
Reescrevemos \(\frac{1}{27}\) como uma potência de base 3:
\( 3^x = \frac{1}{3^3} = 3^{-3} \)
**Assim**, igualamos os expoentes e concluimos que \(x = -3\).
Aplicações da Função Exponencial
**Eventualmente**, as funções exponenciais têm uma ampla gama de aplicações práticas. **A princípio**, na biologia, são usadas para modelar o crescimento de populações (como bactérias e outros organismos) e o decaimento radioativo.
**Atualmente**, na economia, são utilizadas no cálculo de juros compostos, onde o montante cresce exponencialmente ao longo do tempo. **Além disso**, na informática, são usadas em algoritmos de crescimento de complexidade.
**De acordo com** a física, também existem várias aplicações, por exemplo, no resfriamento de objetos e no cálculo da carga e descarga de capacitores. **Portanto**, as funções exponenciais são essenciais para descrever muitos fenômenos do nosso dia a dia.
Exercícios Propostos
**Agora**, que já estudamos os conceitos sobre funções exponenciais, vamos praticar com alguns exercícios. **Dessa maneira**, você poderá fixar o conteúdo e aprofundar seu conhecimento.
1. Qual o valor de \(f(2)\) na função \(f(x) = 3^x\)?
- a) 6
- b) 9
- c) 27
- d) 81
2. Qual a base da função exponencial \(g(x) = 5^x\)?
- a) x
- b) 5
- c) 5x
- d) 25
3. Resolva a equação exponencial \(2^x = 32\).
- a) 4
- b) 5
- c) 6
- d) 7
4. Qual o valor de \(f(0)\) para a função \(f(x) = 7^x\)?
- a) 0
- b) 1
- c) 7
- d) 49
5. A função \(f(x) = 0.5^x\) é:
- a) Crescente
- b) Decrescente
- c) Constante
- d) Não definida
6. Determine a solução da equação \(5^x = 125\).
- a) 2
- b) 3
- c) 4
- d) 5
7. O gráfico da função \(f(x) = e^x\) é:
- a) Decrescente
- b) Crescente
- c) Uma reta horizontal
- d) Uma reta vertical
8. Resolva a equação \( \left(\frac{1}{2}\right)^x = 8\).
- a) -3
- b) 3
- c) -2
- d) 2
**Enfim**, chegamos ao final deste artigo sobre funções exponenciais. **Espero que**, agora, você tenha compreendido a definição, o gráfico, as propriedades e as aplicações dessas funções tão importantes. **Lembre-se** de se inscrever em nosso canal no YouTube Matemática Explorada para mais conteúdos de matemática!

Deixe um comentário