Olá, estudante de matemática! Prepare-se para embarcar em mais uma jornada fascinante pelo universo das funções. Anteriormente, exploramos as funções exponenciais e, ademais, como elas moldam diversos fenômenos ao nosso redor. Contudo, hoje, vamos dar um passo adiante e desvendar o mistério das funções logarítmicas. Afinal, elas são as “irmãs” inversas das exponenciais e, por isso, desempenham um papel crucial na matemática e em várias outras áreas.
O que são Funções Logarítmicas?
Primeiramente, vamos entender a definição. Em resumo, a função logarítmica é a inversa da função exponencial. Em outras palavras, se a função exponencial nos leva de um valor para sua potência, a função logarítmica nos traz de volta ao expoente.
Analogamente, imagine que você tem uma potência como \(a^c = b\). A função logarítmica, nesse sentido, busca o valor do expoente \(c\). Formalmente, escrevemos isso como \(\log_a(b) = c\). Em outras palavras, “o logaritmo de \(b\) na base \(a\) é igual a \(c\), se, e somente se, \(a^c = b\)”.
Nessa representação, temos:
- \(a\): a base do logaritmo. Essa base deve ser sempre um número positivo e diferente de 1 (ou seja, \(a > 0\) e \(a \neq 1\)).
- \(b\): o logaritmando. Esse valor deve ser sempre positivo (ou seja, \(b > 0\)).
- \(c\): o logaritmo. É o expoente ao qual elevamos a base \(a\) para obter o logaritmando \(b\).
Por exemplo, se temos \(2^3 = 8\), então, logaritmicamente, podemos escrever \(\log_2(8) = 3\). Isso significa que o expoente que, quando aplicado à base 2, resulta em 8 é 3.
Em síntese, essa relação inversa é a chave para entender a importância da função logarítmica.
Tipos de Logaritmos
Principalmente, existem dois tipos de logaritmos que usamos com mais frequência:
- Logaritmo Decimal: Também chamado de logaritmo de base 10. A notação é simplesmente “log”, ou seja, \(\log(x)\) significa \(\log_{10}(x)\).
- Logaritmo Natural ou Neperiano: Sua base é o número irracional \(e\), aproximadamente 2.71828. A notação para ele é “ln”, ou seja, \(\ln(x)\) significa \(\log_e(x)\).
Além disso, existem logaritmos em outras bases, mas os mais comuns são os de base 10 e base \(e\).
O Gráfico da Função Logarítmica
A representação gráfica de uma função logarítmica nos permite visualizar seu comportamento. Em outras palavras, um gráfico típico de função logarítmica \(f(x) = \log_a(x)\) tem as seguintes características:
- Assíntota Vertical: O gráfico se aproxima, mas nunca toca, o eixo y. Isso ocorre porque o logaritmando (x) deve ser sempre maior que 0. A reta \(x=0\) é uma assíntota vertical.
- Ponto de Interseção com o Eixo x: O gráfico cruza o eixo x no ponto (1,0), pois \(\log_a(1) = 0\) para qualquer base \(a\).
- Crescimento: Se a base \(a\) for maior que 1 (\(a > 1\)), a função será crescente. Ou seja, à medida que \(x\) aumenta, \(f(x)\) também aumenta.
- Decrescimento: Se a base \(a\) estiver entre 0 e 1 (\(0 < a < 1\)), a função será decrescente. Isto é, à medida que \(x\) aumenta, \(f(x)\) diminui.
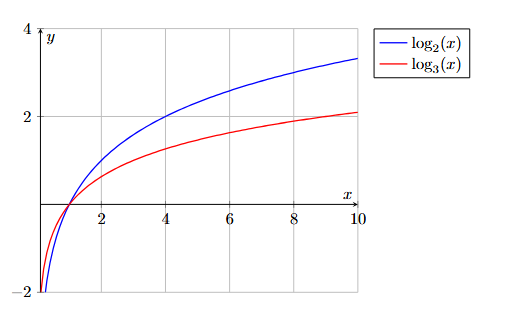
Figura 1: Gráficos de funções logarítmicas com bases diferentes.
Certamente, comparar o gráfico de uma função logarítmica com o de sua inversa (função exponencial) pode ajudar a entender melhor sua relação. Em geral, os gráficos são reflexos um do outro em relação à reta \(y = x\).
Propriedades Operatórias dos Logaritmos
Ainda mais, os logaritmos possuem algumas propriedades importantes que facilitam os cálculos e manipulações. Primordialmente, essas propriedades são derivadas da definição e das propriedades das potências:
- Logaritmo de um Produto: \(\log_a(x \cdot y) = \log_a(x) + \log_a(y)\)
Em outras palavras, o logaritmo de um produto é a soma dos logaritmos dos fatores.
- Logaritmo de um Quociente: \(\log_a(\frac{x}{y}) = \log_a(x) – \log_a(y)\)
Isto é, o logaritmo de um quociente é a diferença entre o logaritmo do numerador e o logaritmo do denominador.
- Logaritmo de uma Potência: \(\log_a(x^n) = n \cdot \log_a(x)\)
Em suma, o logaritmo de uma potência é o produto do expoente pelo logaritmo da base da potência.
- Mudança de Base: \(\log_a(x) = \frac{\log_c(x)}{\log_c(a)}\)
Essa propriedade permite calcular o logaritmo em qualquer base usando outra base conhecida (usualmente, base 10 ou base \(e\)).
Por exemplo, para calcular \(\log_2(16)\), podemos notar que \(16 = 2^4\), e então \(\log_2(16) = \log_2(2^4) = 4 \cdot \log_2(2) = 4 \cdot 1 = 4\).
Aplicações das Funções Logarítmicas
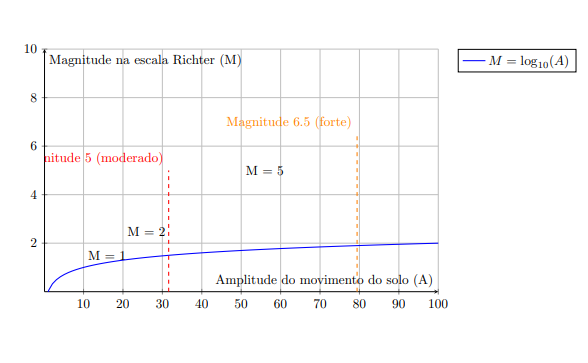
Figura 2: A escala Richter, uma aplicação prática dos logaritmos, mede a magnitude dos terremotos.
Eventualmente, as funções logarítmicas encontram aplicações em diversas áreas. A saber, algumas delas são:
- Escala Richter: Mede a magnitude de terremotos.
- Escala de pH: Determina a acidez ou basicidade de uma solução.
- Cálculo de Juros Compostos: Logaritmos são usados para calcular o tempo necessário para um investimento atingir uma meta.
- Astronomia: A magnitude das estrelas é medida em uma escala logarítmica.
Conforme podemos observar, as funções logarítmicas desempenham um papel crucial em várias áreas do conhecimento.
Um Pouco de História
Primordialmente, o conceito de logaritmo foi desenvolvido independentemente por John Napier, um matemático escocês, e Joost Bürgi, um relojoeiro suíço, no século XVI. No entanto, foi Napier quem publicou os primeiros trabalhos sobre o tema em 1614, com seu livro “Mirifici Logarithmorum Canonis Descriptio”. Nesse sentido, a invenção dos logaritmos revolucionou o cálculo, facilitando operações complexas como multiplicação e divisão. Outrossim, o trabalho de Napier foi fundamental para o desenvolvimento da ciência e tecnologia.
Exercícios Propostos
1. Qual é o valor de \(\log_3(81)\)?
a) 2
b) 3
c) 4
d) 5
Resposta: c) 4
Solução: Precisamos encontrar o expoente que, quando aplicado a 3, resulta em 81. Como \(3^4 = 81\), então \(\log_3(81) = 4\).
2. Se \(\log_2(x) = 5\), qual é o valor de \(x\)?
a) 10
b) 25
c) 32
d) 64
Resposta: c) 32
Solução: Da definição de logaritmo, sabemos que \(\log_2(x) = 5\) implica \(2^5 = x\). Assim, \(x = 32\).
3. Qual das seguintes alternativas representa a propriedade do logaritmo de um produto?
a) \(\log_a(x/y) = \log_a(x) – \log_a(y)\)
b) \(\log_a(x \cdot y) = \log_a(x) + \log_a(y)\)
c) \(\log_a(x^n) = n \cdot \log_a(x)\)
d) \(\log_a(x) = \frac{\log_c(x)}{\log_c(a)}\)
Resposta: b) \(\log_a(x \cdot y) = \log_a(x) + \log_a(y)\)
Solução: A propriedade do logaritmo de um produto afirma que o logaritmo de um produto é a soma dos logaritmos dos fatores.
4. Calcule \(\log_{10}(1000) + \log_{10}(0.01)\)
a) 1
b) 2
c) 3
d) 4
Resposta: a) 1
Solução: \(\log_{10}(1000) = 3\) (pois \(10^3 = 1000\)) e \(\log_{10}(0.01) = -2\) (pois \(10^{-2} = 0.01\)). Assim, \(3 + (-2) = 1\).
5. Qual é a base do logaritmo natural?
a) 2
b) 10
c) \(e\)
d) 3
Resposta: c) \(e\)
Solução: O logaritmo natural, também chamado de neperiano, tem como base o número irracional \(e\), aproximadamente 2.71828.
6. Utilizando a propriedade de mudança de base, transforme \(\log_2(5)\) para logaritmo de base 10.
a) \(\frac{\log(2)}{\log(5)}\)
b) \(\frac{\log(5)}{\log(2)}\)
c) \(\log(2) – \log(5)\)
d) \(\log(5) + \log(2)\)
Resposta: b) \(\frac{\log(5)}{\log(2)}\)
Solução: A fórmula de mudança de base é \(\log_a(x) = \frac{\log_c(x)}{\log_c(a)}\). Assim, \(\log_2(5) = \frac{\log(5)}{\log(2)}\).
7. Simplifique a expressão: \( \log_3(9) + \log_3(27) – \log_3(81) \)
a) 2
b) 1
c) 0
d) -1
Resposta: b) 1
Solução: \(\log_3(9) = 2\), \(\log_3(27) = 3\) e \(\log_3(81) = 4\). Portanto, \(2 + 3 – 4 = 1\).
8. Se \( \ln(x) = 2\), determine o valor de \(x\).
a) \(2\)
b) \(e^2\)
c) \(10^2\)
d) \(2e\)
Resposta: b) \(e^2\)
Solução: Pela definição do logaritmo, temos que \(\ln(x) = \log_e(x) = 2\). Portanto, \(x = e^2\).
Conclusão
Em conclusão, as funções logarítmicas são ferramentas poderosas com aplicações que vão muito além da matemática. Atualmente, seu entendimento é fundamental para a compreensão de diversos fenômenos naturais e tecnológicos. Acima de tudo, lembre-se que a prática leva à perfeição. Portanto, explore os conceitos e faça muitos exercícios para dominar esse tema.
Para complementar seus estudos, não deixe de conferir nossos artigos anteriores sobre função modular e funções exponenciais. Além disso, explore nosso canal no YouTube Matemática Explorada, onde você encontrará mais conteúdos didáticos e interessantes!

Deixe um comentário