Primordialmente, quando nos aventuramos pelo universo da matemática, encontramos uma miríade de conceitos que, a princípio, podem parecer abstratos e complexos. Contudo, por trás de cada definição, existe um mundo de aplicações práticas e ideias fascinantes. Nesse sentido, um dos conceitos mais importantes e versáteis na matemática são as funções. Assim, este artigo tem o propósito de desvendar o mistério por trás das funções, mostrando o que são e como elas surgem no contexto das relações matemáticas.
Sobretudo, as funções são ferramentas poderosas que nos permitem modelar e compreender uma ampla gama de fenômenos do mundo real. Inegavelmente, desde o movimento de um carro até o crescimento de uma população, as funções estão presentes em todos os cantos, proporcionando uma estrutura matemática para analisar e prever comportamentos. Então, prepare-se para embarcar nesta jornada de descoberta e entender a beleza e a utilidade das funções!
Introdução e Motivação: Onde as Funções Se Escondem?
A princípio, ao pensarmos em matemática, muitas vezes visualizamos números, equações e gráficos. Entretanto, a matemática vai muito além de apenas manipular símbolos; ela busca entender as relações entre os objetos e as grandezas que nos cercam. Dessa forma, as funções, por exemplo, são a própria representação dessas relações, permitindo que possamos expressar e analisar como uma quantidade se modifica em relação a outra.
Analogamente, podemos pensar em uma função como uma máquina: você insere algo (uma entrada), a máquina processa essa entrada e devolve algo (uma saída). Por exemplo, imagine uma máquina que calcula o dobro de qualquer número que você inserir. Assim, se você inserir o número 2, a máquina retornará 4. Se você inserir 5, ela retornará 10. Afinal, essa máquina está definindo uma função que relaciona um número a seu dobro!
Aliás, as funções estão presentes em nosso dia a dia de maneiras surpreendentes. De fato, a relação entre a quantidade de gasolina em um tanque e a distância que um carro pode percorrer é uma função. Similarmente, a relação entre o tempo e a posição de um objeto em movimento também pode ser descrita por uma função. Portanto, ao entendermos as funções, começamos a compreender melhor o mundo ao nosso redor.
Relações entre Conjuntos: A Base das Funções
Antes de mais nada, para entender o que é uma função, precisamos falar sobre conjuntos. Em resumo, um conjunto é simplesmente uma coleção de objetos distintos, que podem ser números, pessoas, ou qualquer outra coisa. Por exemplo, podemos ter o conjunto A = {1, 2, 3} e o conjunto B = {a, b, c}. A saber, podemos estabelecer relações entre esses conjuntos.
Nesse sentido, uma relação entre dois conjuntos A e B é, de modo geral, uma forma de associar elementos de A a elementos de B. Assim, podemos representar uma relação por meio de diagramas. Veja o exemplo abaixo, que ilustra uma relação entre dois conjuntos.
Exemplo de Relação
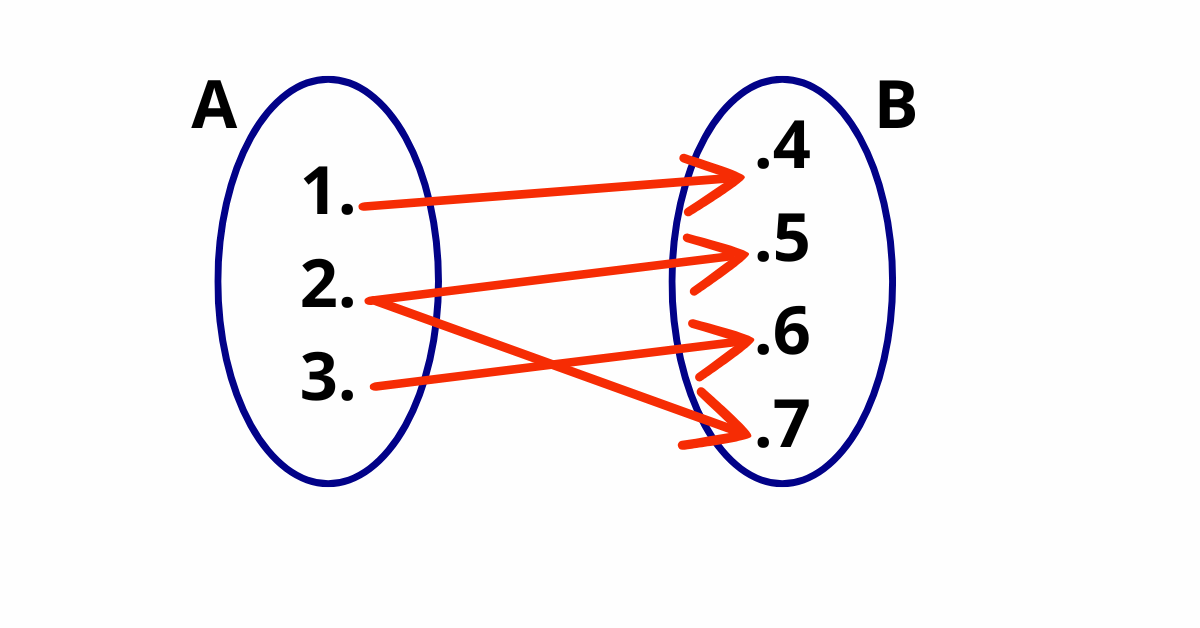
Considere o conjunto A = {1, 2, 3} e o conjunto B = {4, 5, 6, 7}. Uma possível relação entre A e B é:
1 está relacionado a 4.
2 está relacionado a 5 e 7.
3 está relacionado a 6.
Nesse exemplo, o elemento 2 está relacionado com dois elementos em B. Abaixo, você poderá adicionar uma imagem que ilustra esse diagrama de flechas, com texto alternativo “Diagrama de flechas representando uma relação entre dois conjuntos, onde o elemento 2 de A se relaciona com os elementos 5 e 7 de B”.
A Definição de Função: O Que a Torna Especial?
De fato, nem toda relação entre conjuntos é uma função. Portanto, uma função é um tipo especial de relação que satisfaz uma regra crucial: cada elemento do conjunto de partida (o domínio da função) deve estar associado a um único elemento do conjunto de chegada (o contradomínio da função). Ou seja, não pode haver uma “saída dupla” para uma mesma entrada.
Em outras palavras, para que uma relação seja considerada uma função, cada elemento do domínio deve ter exatamente uma imagem no contradomínio. Ademais, essa propriedade é conhecida como a “unicidade da imagem”. Assim sendo, se um elemento do domínio tem mais de uma imagem no contradomínio, a relação não é uma função.
Exemplo de Relação que NÃO é uma Função
Vamos retomar o exemplo anterior. O elemento 2 do conjunto A está associado a dois elementos do conjunto B (5 e 7). Dessa forma, essa relação não é uma função. Abaixo, você poderá adicionar uma imagem que ilustra esse diagrama de flechas, com texto alternativo “Diagrama de flechas representando uma relação que não é uma função, onde o elemento 2 de A se relaciona com os elementos 5 e 7 de B.”

Exemplo de Relação que É uma Função
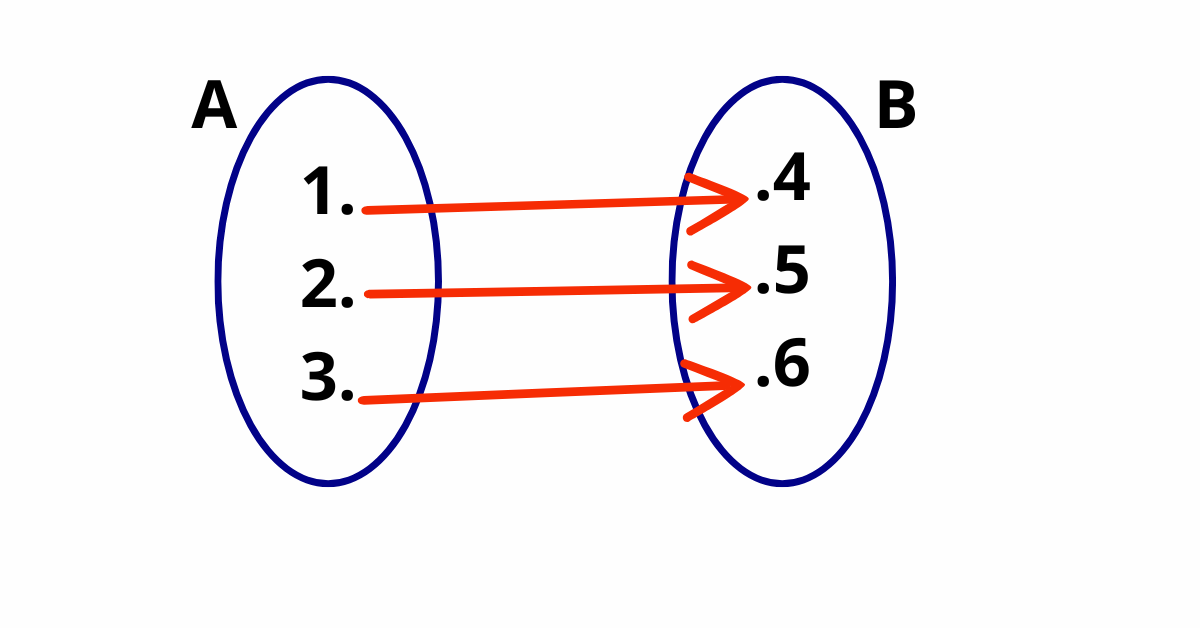
Agora, considere a seguinte relação entre A = {1, 2, 3} e B = {4, 5, 6}:
1 está relacionado com 4.
2 está relacionado com 5.
3 está relacionado com 6.
Nesse caso, cada elemento do conjunto A está associado a um único elemento do conjunto B. Portanto, essa relação é uma função.
Abaixo, você poderá adicionar uma imagem que ilustra esse diagrama de flechas, com texto alternativo “Diagrama de flechas representando uma relação que é uma função, onde cada elemento de A se relaciona com um único elemento de B”.
Importante: Uma função pode ter dois elementos diferentes do domínio que são associados ao mesmo elemento do contradomínio. Ou seja, o que não pode acontecer é um único elemento do domínio ser associado a dois ou mais elementos diferentes do contradomínio.
Exemplos Simples para Clarificar a Ideia
Para ilustrar, vamos explorar mais alguns exemplos simples que ajudarão a solidificar o conceito de função.
Exemplo 1: A Função que Dobra Números
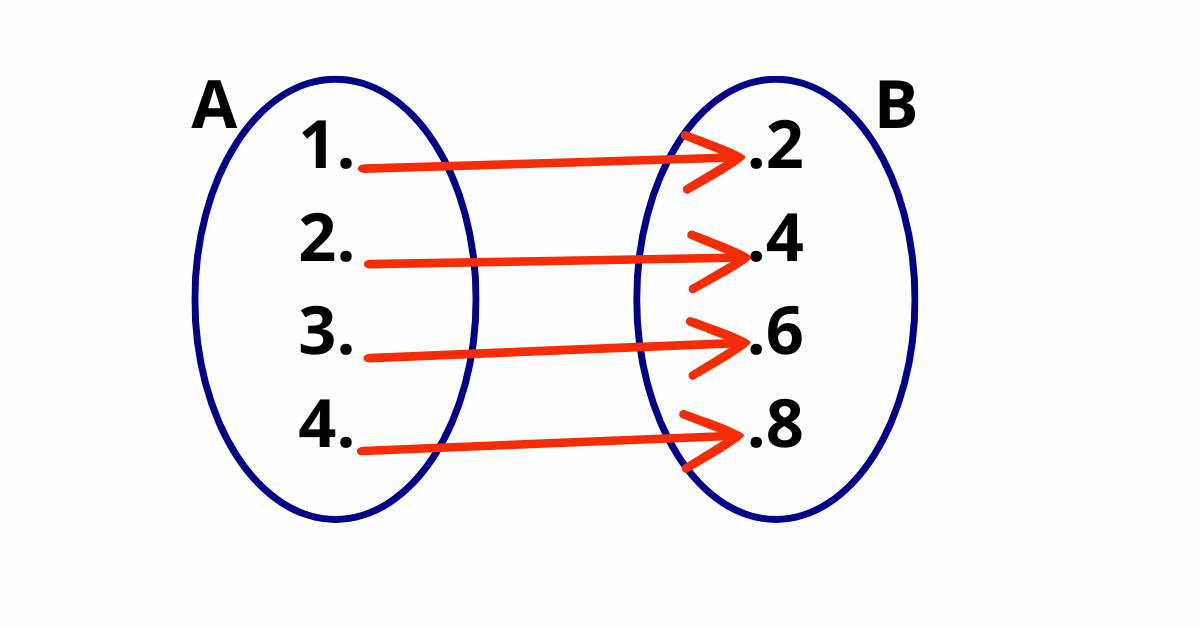
Considere o conjunto de entrada A = {1, 2, 3, 4} e o conjunto de saída B = {2, 4, 6, 8, 9}. Nesse contexto, podemos definir uma função que dobra cada número do conjunto A. Assim:
1 está relacionado com 2
2 está relacionado com 4
3 está relacionado com 6
4 está relacionado com 8
Logo, essa relação é uma função, visto que cada número do conjunto de entrada é associado a um único número do conjunto de saída.
Abaixo, você poderá adicionar uma imagem que ilustra esse diagrama de flechas, com texto alternativo “Diagrama de flechas representando a função que dobra números do conjunto A no conjunto B”
Exemplo 2: A Relação de Idade com Pessoas
Por outro lado, imagine uma relação entre um conjunto de pessoas e suas respectivas idades. A saber, cada pessoa tem uma idade específica, portanto, essa relação é uma função. Por exemplo, se no conjunto de pessoas temos: Maria, João e Ana, e suas idades são respectivamente 20, 25 e 20, a relação é uma função (duas pessoas podem ter a mesma idade, o que não pode acontecer é uma pessoa ter duas idades).
Conclusão
Em conclusão, as funções são ferramentas poderosas na matemática, que nos permitem expressar e analisar relações entre conjuntos de forma precisa e eficiente. Acima de tudo, ao entendermos a definição e os conceitos básicos por trás das funções, abrimos portas para um universo vasto de possibilidades, que vão desde a modelagem de fenômenos naturais até a resolução de problemas complexos. Todavia, este é apenas o primeiro passo em nossa jornada de descoberta. No entanto, se você deseja explorar mais sobre o universo da matemática, te convido a conhecer nosso canal no YouTube, Matemática Explorada, que oferece diversos conteúdos sobre matemática de forma didática e envolvente. Além disso, não deixe de conferir outros artigos do nosso blog, como nosso guia completo sobre Progressão Aritmética e nosso artigo sobre Análise Combinatória e Chances em Jogos de Loteria. Assim, continue conosco para aprofundar seus conhecimentos e desvendar os mistérios das funções!

Deixe um comentário