**Primeiramente,** vamos relembrar o conceito de função que abordamos no artigo Introdução às Funções Matemáticas. Afinal, uma função é uma relação entre dois conjuntos, onde cada elemento do primeiro conjunto (o domínio) está associado a um único elemento do segundo conjunto (o contradomínio). Ademais, vimos que as funções podem ser representadas de diversas maneiras, conforme exploramos em Como Representar Funções. Agora, estamos prontos para dar o próximo passo e explorar um tipo especial de função: a função quadrática.
**Anteriormente**, estudamos as funções lineares e afins, que são funções de primeiro grau. **No entanto**, o mundo das funções é muito mais vasto e existem funções que se comportam de maneira bem diferente, como as funções quadráticas. **Assim**, elas são fundamentais em diversos ramos da matemática, física e outras áreas do conhecimento.
Definição Formal da Função Quadrática
**Sobretudo**, a função quadrática, ou função polinomial do 2º grau, é definida pela seguinte lei de formação:
\(f(x) = ax^2 + bx + c\)
Nessa expressão, \(a\), \(b\) e \(c\) são coeficientes reais, sendo que \(a\) deve ser diferente de zero (\(a \neq 0\)). **Afinal**, se \(a\) fosse igual a zero, a função se transformaria em uma função linear ou afim, que já estudamos. **Portanto**, o coeficiente \(a\) é o que garante que a função seja realmente quadrática.
Vamos entender o que cada coeficiente representa:
- \(a\): Determina a concavidade da parábola, que veremos a seguir. Se \(a > 0\), a concavidade é para cima (em forma de “U”), e se \(a < 0\), a concavidade é para baixo (em forma de "∩").
- \(b\): Influencia a posição do vértice da parábola no eixo x.
- \(c\): Indica onde a parábola corta o eixo y. **Em outras palavras**, é o valor de \(f(0)\).
**Por exemplo**, na função \(f(x) = 2x^2 – 3x + 1\), temos \(a = 2\), \(b = -3\) e \(c = 1\). **Analogamente**, na função \(g(x) = -x^2 + 4\), temos \(a = -1\), \(b = 0\) e \(c = 4\).
O Gráfico da Função Quadrática: a Parábola
**Certamente**, o gráfico de uma função quadrática é sempre uma parábola. **Aliás**, uma parábola é uma curva em forma de “U” (concavidade para cima) ou “∩” (concavidade para baixo). **De acordo com** o valor de \(a\), podemos determinar a concavidade:
- Se \(a > 0\), a parábola tem concavidade para cima.
- Se \(a < 0\), a parábola tem concavidade para baixo.
**Além disso**, a parábola possui um ponto especial chamado de vértice, que representa o valor máximo (se a concavidade for para baixo) ou mínimo (se a concavidade for para cima) da função. **Similarmente**, o vértice é o ponto de “mudança” na direção da parábola.
**Todavia**, a parábola também possui um eixo de simetria, que é uma reta vertical que passa pelo vértice. **Isto é**, a parábola é simétrica em relação a esse eixo.
Para construir um gráfico, **primeiramente**, podemos escolher alguns valores de \(x\) e calcular os correspondentes valores de \(f(x)\). **Em seguida**, plotamos esses pontos no plano cartesiano e traçamos a parábola, **conforme** o exemplo abaixo:
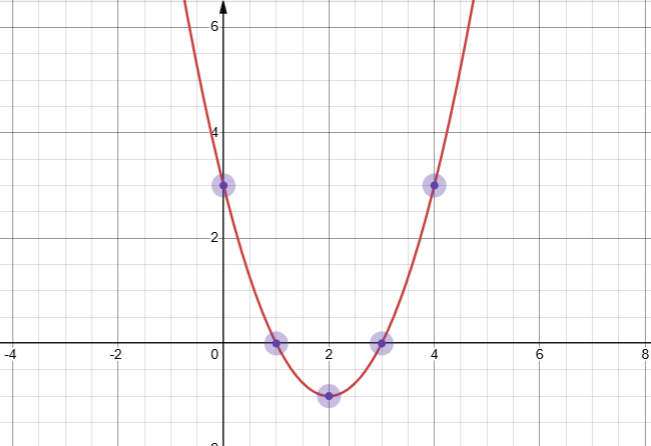
Para a função \( f(x) = x^2 – 4x + 3\), podemos calcular:
- Se \(x=0\), então \(f(0) = (0)^2 – 4(0) + 3 = 3\)
- Se \(x=1\), então \(f(1) = (1)^2 – 4(1) + 3 = 0\)
- Se \(x=2\), então \(f(2) = (2)^2 – 4(2) + 3 = -1\)
- Se \(x=3\), então \(f(3) = (3)^2 – 4(3) + 3 = 0\)
- Se \(x=4\), então \(f(4) = (4)^2 – 4(4) + 3 = 3\)
**Em virtude disso**, podemos construir um gráfico com esses pontos.
Zeros da Função Quadrática (Raízes)
**Logo**, os zeros ou raízes da função quadrática são os valores de \(x\) para os quais \(f(x) = 0\). **Em outras palavras**, são os pontos onde a parábola corta o eixo x.
Para encontrar os zeros, devemos resolver a equação \(ax^2 + bx + c = 0\). **Assim**, podemos utilizar a famosa fórmula de Bhaskara:
\(x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}\)
**Contudo**, o termo \( \Delta = b^2 – 4ac \), que está dentro da raiz quadrada, é chamado de discriminante. **Então**, ele indica quantos zeros a função possui:
- Se \( \Delta > 0\), a função tem duas raízes reais e distintas.
- Se \( \Delta = 0\), a função tem uma raiz real (raiz dupla).
- Se \( \Delta < 0\), a função não tem raízes reais.
**Por exemplo**, vamos calcular as raizes da função \( f(x) = x^2 – 5x + 6\):
Temos: \(a = 1, b = -5\) e \(c = 6\), logo \(\Delta = (-5)^2 – 4(1)(6) = 25 – 24 = 1\)
Aplicando a fórmula de Bhaskara:
\(x = \frac{-(-5) \pm \sqrt{1}}{2(1)} = \frac{5 \pm 1}{2}\)
**Dessa forma**, temos as duas raízes:
\(x_1 = \frac{5 + 1}{2} = 3 \) e \(x_2 = \frac{5 – 1}{2} = 2 \)
**Nesse sentido**, a parábola corta o eixo x nos pontos \(x = 2\) e \(x = 3\).
Aplicações da Função Quadrática
**Eventualmente**, as funções quadráticas estão presentes em diversas áreas do conhecimento. **A princípio**, na física, elas descrevem o movimento de projéteis (como bolas arremessadas), onde a trajetória segue uma parábola devido à gravidade. **Analogamente**, na engenharia, são utilizadas no design de pontes e antenas parabólicas, pois a parábola tem propriedades de foco.
**Atualmente**, na economia, são utilizadas para modelar custos e receitas, onde, **por exemplo**, pode ser identificado o ponto de lucro máximo. **Assim**, também são utilizadas em muitos algoritmos de otimização. **Por fim**, esses são apenas alguns exemplos, e as funções quadráticas têm uma vasta gama de aplicações em diversas áreas.
Exercícios Propostos
**Agora**, vamos praticar o que aprendemos com alguns exercícios. **Dessa maneira**, você poderá fixar o conteúdo e aplicar o que foi ensinado. **Afinal**, a prática leva à perfeição!
1. Dada a função \(f(x) = -2x^2 + 8x – 6\), qual o valor dos coeficientes a, b e c, respectivamente?
- a) 2, 8, -6
- b) -2, 8, -6
- c) -2, -8, 6
- d) 2, -8, -6
2. Qual a concavidade da parábola da função \(g(x) = 3x^2 – 5x + 2\)?
- a) Concavidade para cima.
- b) Concavidade para baixo.
- c) Não é uma parábola.
- d) Nenhuma das alternativas
3. Determine os zeros da função \(h(x) = x^2 – 4x + 4\).
- a) 2 e -2.
- b) 4.
- c) Apenas 2.
- d) Não tem raízes reais.
4. Qual das seguintes funções possui concavidade para baixo?
- a) \(f(x) = 2x^2 – 3x + 1\)
- b) \(g(x) = -x^2 + 4x – 2\)
- c) \(h(x) = x^2 + 2x + 3\)
- d) \(j(x) = 3x^2 + x – 5\)
5. Determine os zeros da função \(k(x) = x^2 – 6x + 8\).
- a) 1 e 2
- b) 2 e 4
- c) 3 e 5
- d) 4 e 6
6. Qual o valor de \(f(2)\) na função \( f(x) = -x^2 + 5x – 6\)?
- a) -2
- b) 0
- c) 1
- d) 2
7. Dada a função \(f(x) = x^2 – 6x + 9\), a parábola intercepta o eixo x em:
- a) Dois pontos distintos.
- b) Um único ponto.
- c) Não intercepta o eixo x.
- d) Nenhuma das alternativas.
8. A função \( p(x) = x^2 + 2x + 3\) possui:
- a) Dois zeros reais.
- b) Um zero real.
- c) Nenhum zero real.
- d) Infinitos zeros reais
**Enfim**, chegamos ao final deste artigo sobre funções quadráticas. **Espero que**, agora, você tenha uma compreensão clara sobre o que são, como são representadas graficamente e quais são suas aplicações. **Por fim**, continue explorando os diversos assuntos matemáticos em nosso site e não se esqueça de conferir mais conteúdos em meu canal do YouTube Matemática Explorada.

Deixe um comentário