Olá, estudante de matemática! Se você já explorou as funções exponenciais e logarítmicas, está pronto para dar o próximo passo: as funções trigonométricas. Essas funções, afinal, são fundamentais para descrever fenômenos periódicos e oscilatórios, desde o movimento de um pêndulo até as ondas de rádio. Neste artigo, portanto, vamos mergulhar no fascinante mundo das funções trigonométricas, desvendando seus conceitos, gráficos e aplicações.
O que são Funções Trigonométricas?
Em resumo, as funções trigonométricas são funções matemáticas que relacionam os ângulos de um triângulo com as razões de seus lados. Contudo, essas funções vão muito além dos triângulos, pois elas se aplicam a qualquer tipo de ângulo, e são definidas utilizando o círculo trigonométrico. Principalmente, as funções trigonométricas básicas são o seno, o cosseno e a tangente, além de suas inversas: a cossecante, a secante e a cotangente.
Analogamente, as funções trigonométricas são utilizadas em diversas áreas, como física, engenharia, música, computação gráfica, entre outras. Em outras palavras, a importância delas é inegável.
Anteriormente, ao estudarmos trigonometria, vimos que as razões trigonométricas são definidas em triângulos retângulos. Em suma, as funções trigonométricas expandem esse conceito, aplicando-o a qualquer ângulo, e são a base para entender diversos fenômenos oscilatórios. Antes de mais nada, vamos relembrar alguns conceitos básicos:
- Cateto Oposto: Lado do triângulo que está oposto ao ângulo em questão.
- Cateto Adjacente: Lado do triângulo que está ao lado do ângulo em questão (e não é a hipotenusa).
- Hipotenusa: Lado do triângulo oposto ao ângulo reto (o maior lado).
O Círculo Trigonométrico: A Base das Funções Trigonométricas
Primeiramente, o círculo trigonométrico é uma ferramenta fundamental para entender as funções trigonométricas. Certamente, ele é um círculo cujo raio tem comprimento igual a 1, e que está centrado na origem de um plano cartesiano.
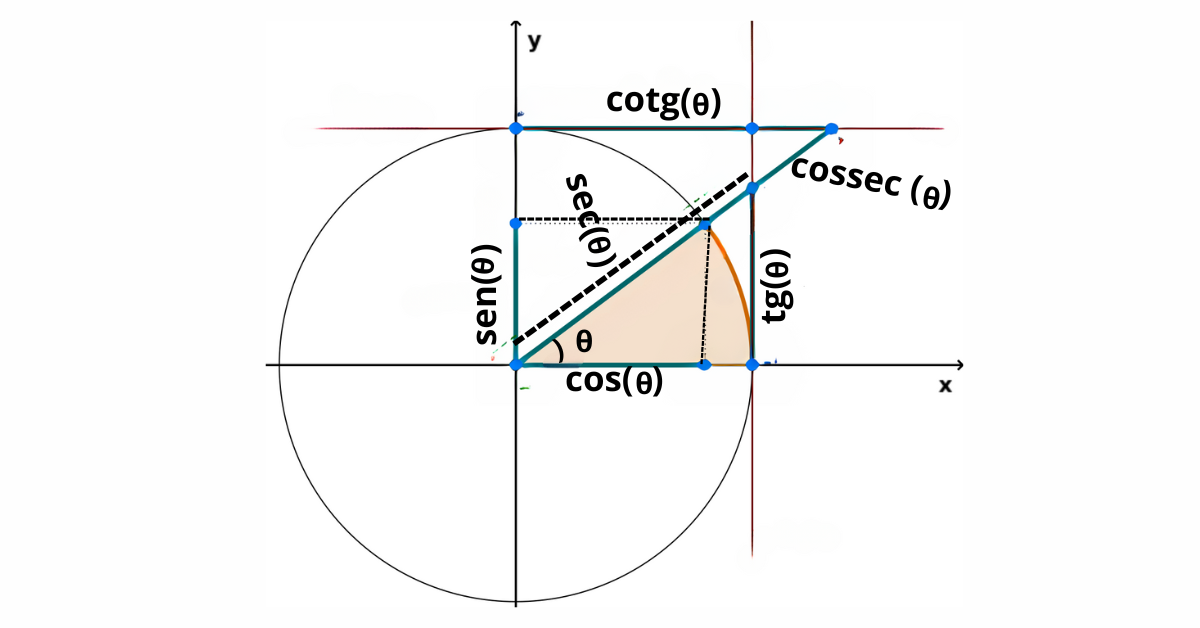
Figura 1: O círculo trigonométrico e suas relações com as funções seno e cosseno.
Nesse sentido, o eixo horizontal representa o cosseno e o eixo vertical representa o seno de um ângulo, o qual é medido no sentido anti-horário a partir do eixo horizontal. Assim sendo, os ângulos podem ser medidos em graus ou radianos, sendo 360 graus ou 2π radianos equivalentes a uma volta completa no círculo.
A saber, as funções trigonométricas são definidas para qualquer ângulo, independentemente de estar em um triângulo. Contudo, o círculo trigonométrico nos ajuda a visualizar como o seno, o cosseno e a tangente variam à medida que o ângulo muda.
Ademais, é importante notar que, em cada quadrante, o seno e o cosseno podem ter sinais diferentes. O seno é positivo nos quadrantes I e II, e negativo nos quadrantes III e IV. O cosseno é positivo nos quadrantes I e IV, e negativo nos quadrantes II e III. A tangente, por outro lado, é positiva nos quadrantes I e III e negativa nos quadrantes II e IV.
Definição das Funções Trigonométricas
Dessa forma, vamos definir formalmente as funções trigonométricas básicas. Em outras palavras, no círculo trigonométrico, para um ângulo \( \theta \):
- Seno (sen): É a coordenada y do ponto no círculo, ou seja, \( sen(\theta) = y\).
- Cosseno (cos): É a coordenada x do ponto no círculo, ou seja, \( cos(\theta) = x\).
- Tangente (tan): É a razão entre o seno e o cosseno, ou seja, \( tan(\theta) = \frac{sen(\theta)}{cos(\theta)} \).
Além disso, existem as funções trigonométricas inversas:
- Cossecante (csc): É o inverso do seno, ou seja, \( csc(\theta) = \frac{1}{sen(\theta)} \).
- Secante (sec): É o inverso do cosseno, ou seja, \( sec(\theta) = \frac{1}{cos(\theta)} \).
- Cotangente (cot): É o inverso da tangente, ou seja, \( cot(\theta) = \frac{1}{tan(\theta)} = \frac{cos(\theta)}{sen(\theta)} \).
Conforme podemos observar, as funções trigonométricas são definidas para qualquer ângulo, o que permite que as utilizemos em qualquer situação, não apenas em triângulos retângulos.
Gráficos das Funções Trigonométricas
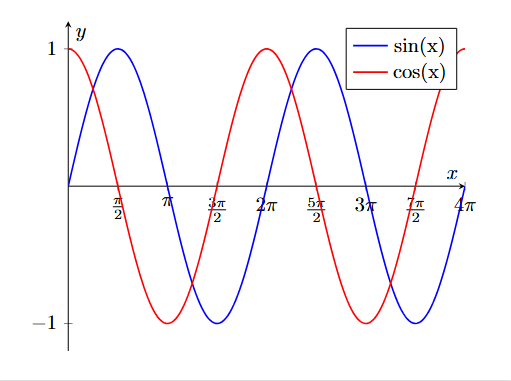
Figura 2: Gráficos das funções seno (em azul) e cosseno (em vermelho).
De maneira idêntica, os gráficos das funções trigonométricas nos ajudam a visualizar como elas variam em função do ângulo. Os gráficos das funções seno e cosseno são ondas periódicas, que repetem seus valores a cada 2π radianos (ou 360 graus).
- Amplitude: A amplitude é a altura máxima que o gráfico atinge em relação ao eixo x. Para seno e cosseno, a amplitude é 1.
- Período: O período é o comprimento do intervalo em que o gráfico se repete. Para seno e cosseno, o período é 2π.
- Frequência: A frequência é o número de repetições do gráfico em um determinado intervalo.
- Deslocamento de Fase: O deslocamento de fase é o deslocamento horizontal do gráfico.
O gráfico da função tangente, em contrapartida, possui assíntotas verticais e se repete a cada π radianos. As funções seno e cosseno variam entre -1 e 1, enquanto a tangente pode assumir qualquer valor.
Identidades Trigonométricas
Além disso, as identidades trigonométricas são relações importantes entre as funções trigonométricas. Uma das identidades mais importantes é a identidade fundamental:
Essa identidade, acima de tudo, deriva do teorema de Pitágoras aplicado ao círculo trigonométrico. Além dessa identidade, existem outras, como as relações entre seno, cosseno e tangente, e as relações entre as funções inversas.
As identidades trigonométricas são importantes para simplificar expressões e resolver equações trigonométricas. Elas nos permitem transformar uma função trigonométrica em outra mais conveniente.
Aplicações das Funções Trigonométricas
As funções trigonométricas, todavia, são encontradas em diversas aplicações do mundo real:
- Física: Movimento harmônico simples (como o pêndulo), ondas sonoras e eletromagnéticas.
- Engenharia: Cálculo de ângulos e distâncias, análise de estruturas e circuitos elétricos.
- Música: Sons e harmônicos, análise de frequências e timbres.
- Astronomia: Movimentos dos astros, localização de estrelas e planetas.
Em suma, as funções trigonométricas são ferramentas essenciais para modelar e entender fenômenos periódicos em diversas áreas.
Um Pouco de História
Primordialmente, o estudo da trigonometria remonta aos tempos antigos, com contribuições significativas de matemáticos gregos como Hiparco de Niceia e Cláudio Ptolomeu. Posteriormente, no mundo islâmico, matemáticos como Al-Khwarizmi e Al-Battani fizeram avanços importantes na área. Eventualmente, no século XV, a trigonometria foi refinada na Europa com o trabalho de matemáticos como Regiomontanus e Nicolau Copérnico.
Assim sendo, a história das funções trigonométricas é uma jornada de descobertas e avanços que moldaram nossa compreensão do mundo.
Exercícios Propostos
1. Qual o valor de \( sen(90^\circ) \)?
a) 0
b) 1
c) -1
d) 0.5
Resposta: b) 1
Solução: No círculo trigonométrico, o seno de 90 graus corresponde ao valor máximo no eixo y, que é 1.
2. Qual o valor de \( cos(180^\circ) \)?
a) 0
b) 1
c) -1
d) 0.5
Resposta: c) -1
Solução: No círculo trigonométrico, o cosseno de 180 graus corresponde ao valor mínimo no eixo x, que é -1.
3. Qual a relação entre \( tan(\theta) \), \( sen(\theta) \) e \( cos(\theta) \)?
a) \( tan(\theta) = sen(\theta) + cos(\theta) \)
b) \( tan(\theta) = sen(\theta) – cos(\theta) \)
c) \( tan(\theta) = \frac{sen(\theta)}{cos(\theta)} \)
d) \( tan(\theta) = \frac{cos(\theta)}{sen(\theta)} \)
Resposta: c) \( tan(\theta) = \frac{sen(\theta)}{cos(\theta)} \)
Solução: A tangente de um ângulo é definida como a razão entre o seno e o cosseno desse mesmo ângulo.
4. Qual o período da função seno?
a) \(\pi\)
b) \(\frac{\pi}{2}\)
c) \(2\pi\)
d) \(3\pi\)
Resposta: c) \(2\pi\)
Solução: O gráfico da função seno se repete a cada 2π radianos.
5. Qual a amplitude da função cosseno?
a) 0
b) 1
c) -1
d) 2
Resposta: b) 1
Solução: A amplitude da função cosseno é a altura máxima que o gráfico atinge em relação ao eixo x, que é 1.
6. Qual a identidade trigonométrica fundamental?
a) \(sen^2(x) – cos^2(x) = 1\)
b) \(sen(x) + cos(x) = 1\)
c) \(sen^2(x) + cos^2(x) = 1\)
d) \(tan^2(x) + 1 = sec^2(x)\)
Resposta: c) \(sen^2(x) + cos^2(x) = 1\)
Solução: A identidade trigonométrica fundamental relaciona o seno e o cosseno de um mesmo ângulo.
7. Se \( sen(x) = 0.6 \), e \( x \) está no primeiro quadrante, qual o valor de \( cos(x) \)?
a) 0.4
b) 0.5
c) 0.8
d) 1
Resposta: c) 0.8
Solução: Usando a identidade fundamental, temos \( cos^2(x) = 1 – sen^2(x) = 1 – (0.6)^2 = 1 – 0.36 = 0.64\). Logo, \( cos(x) = \sqrt{0.64} = 0.8\).
8. Qual é o valor de \( tan(45^\circ) \)?
a) 0
b) 1
c) -1
d) \(\sqrt{3}\)
Resposta: b) 1
Solução: \(tan(45^\circ) = \frac{sen(45^\circ)}{cos(45^\circ)} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1\)
Conclusão
Em conclusão, as funções trigonométricas são ferramentas poderosas para entender e modelar fenômenos periódicos, e são importantíssimas para diversos campos da ciência e da engenharia. Neste artigo, enfim, exploramos os conceitos básicos, os gráficos e algumas das aplicações dessas funções. Todavia, este é apenas o início da sua jornada no mundo da matemática. Por isso, continue estudando e praticando, e você certamente irá dominar este e outros temas.
Para complementar seus estudos, revise nossos artigos anteriores sobre introdução às funções e representação de funções. Além disso, explore nosso canal no YouTube Matemática Explorada, onde você encontrará mais conteúdos didáticos e interessantes!

Deixe um comentário