**Primordialmente**, vamos adentrar no fascinante mundo dos poliedros, figuras geométricas tridimensionais que nos cercam por todos os lados. **Afinal**, desde as estruturas de edifícios até os cristais encontrados na natureza, os poliedros estão presentes em inúmeras formas e contextos. **Assim**, este artigo irá guiá-lo através dos conceitos fundamentais, exemplos práticos e exercícios resolvidos, proporcionando uma compreensão completa sobre esse tema da geometria.
O Que São Poliedros?
**A princípio**, é crucial entender que um poliedro é um sólido geométrico delimitado por faces planas. **Analogamente**, imagine uma caixa: suas laterais, o topo e o fundo são todos planos e, juntos, formam um poliedro. **Aliás**, as faces de um poliedro são polígonos, que se encontram nas arestas e vértices.
**Em outras palavras**, um poliedro é uma figura tridimensional composta por polígonos que se unem para formar uma estrutura fechada. **Além disso**, os poliedros são classificados em diversos tipos, cada um com características próprias e interessantes. **Dessa forma**, entender os poliedros é essencial para quem estuda geometria e suas aplicações.
Elementos de um Poliedro
**Em primeiro lugar**, é importante conhecer os elementos básicos de um poliedro:
- Faces: São os polígonos que formam a superfície do poliedro.
- Arestas: São os segmentos de reta onde duas faces se encontram.
- Vértices: São os pontos onde três ou mais arestas se encontram.
Tipos Principais de Poliedros
**Atualmente**, os poliedros são classificados em dois grandes grupos: os poliedros convexos e os poliedros não convexos (ou côncavos). **Posteriormente**, vamos explorar cada um deles.
Poliedros Convexos
**De fato**, um poliedro convexo é aquele em que qualquer segmento de reta com extremidades no interior do poliedro está inteiramente contido no interior do poliedro. **Em outras palavras**, um poliedro convexo não tem “reentrâncias” ou “cavidades”. **Assim sendo**, eles são mais simples de visualizar e analisar.
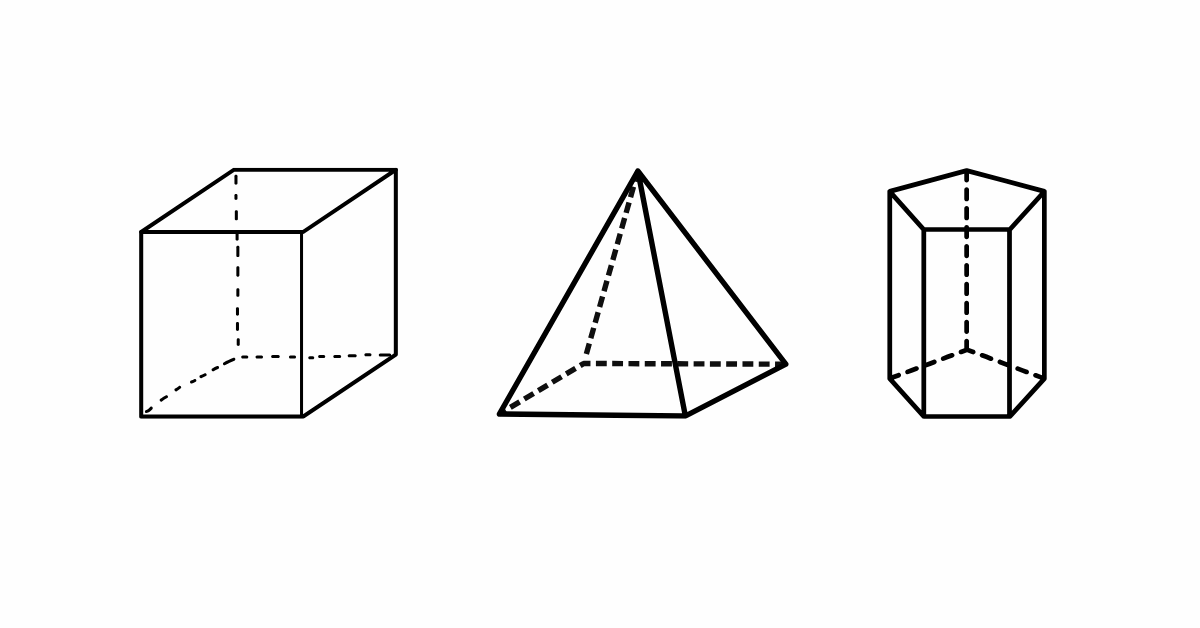
**Por exemplo**, um cubo, uma pirâmide e um prisma são exemplos de poliedros convexos.
Poliedros Não Convexos (Côncavos)
**Por outro lado**, um poliedro não convexo ou côncavo é aquele em que existe pelo menos um segmento de reta com extremidades no interior do poliedro que não está totalmente contido nele. **Nesse sentido**, esses poliedros possuem “reentrâncias”. **Todavia**, eles também são importantes para diversas áreas da matemática.
**A saber**, um poliedro em forma de estrela é um exemplo de poliedro não convexo.

Poliedros de Platão
**Além disso**, dentro dos poliedros convexos, existem os poliedros de Platão, também conhecidos como sólidos platônicos. **Nesse sentido**, esses são poliedros convexos regulares, ou seja, todas as suas faces são polígonos regulares e todos os seus ângulos diedrais são congruentes. **Assim também**, eles são considerados modelos ideais na geometria.
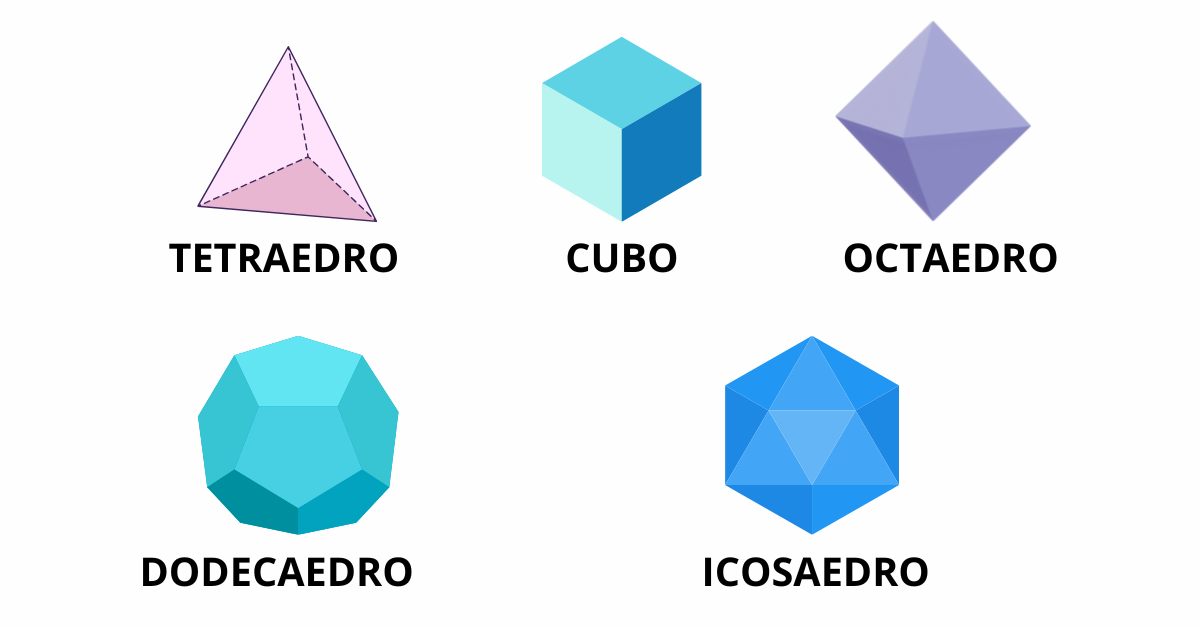
**Sobretudo**, existem apenas cinco poliedros de Platão:
- Tetraedro: 4 faces triangulares.
- Cubo (Hexaedro): 6 faces quadradas.
- Octaedro: 8 faces triangulares.
- Dodecaedro: 12 faces pentagonais.
- Icosaedro: 20 faces triangulares.
**Só para ilustrar**, observe a imagem abaixo dos cinco sólidos platônicos:
Poliedros de Arquimedes
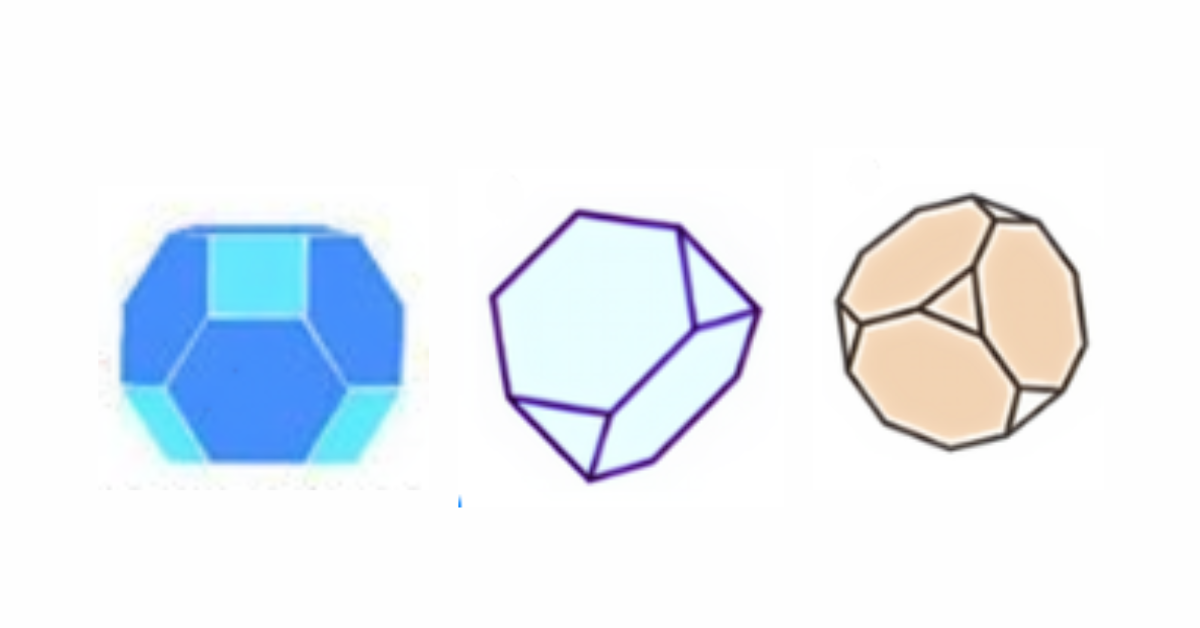
**Eventualmente**, os poliedros de Arquimedes, também conhecidos como poliedros semi-regulares, são poliedros convexos com faces formadas por dois ou mais tipos de polígonos regulares, mas com os mesmos ângulos diedrais. **Similarmente**, eles são uma extensão dos sólidos platônicos, com mais variedade em suas formas. **Diga-se de passagem**, são 13 poliedros de Arquimedes, incluindo o cubo truncado, o icosidodecaedro e outros.
**Para exemplificar**, observe a imagem abaixo de alguns poliedros de Arquimedes:
Relação de Euler
**Certamente**, uma das relações mais importantes sobre os poliedros convexos é a relação de Euler, que conecta o número de vértices (V), arestas (A) e faces (F) de um poliedro:
**Nesse sentido**, essa relação é válida para qualquer poliedro convexo e permite verificar se um conjunto de vértices, arestas e faces forma realmente um poliedro convexo. **Assim**, ela é uma ferramenta fundamental para estudar os poliedros.
A História dos Poliedros
**Antes de tudo**, o estudo dos poliedros remonta à Grécia Antiga. **Principalmente**, os gregos, incluindo Platão e Euclides, já exploravam a beleza e a matemática dessas formas. **Entretanto**, foi com a obra “Os Elementos” de Euclides que os poliedros foram formalmente tratados. **Inegavelmente**, a matemática grega estabeleceu as bases para o estudo dos poliedros.
**Conforme** avançava a matemática, matemáticos como Johannes Kepler e Leonhard Euler trouxeram importantes contribuições para o estudo dos poliedros. **De fato**, Kepler descobriu dois novos poliedros regulares, enquanto Euler estabeleceu a relação que leva seu nome. **Igualmente**, essas descobertas foram cruciais para o desenvolvimento da geometria.
**Aliás**, existem também curiosidades históricas sobre os poliedros. **Por exemplo**, os sólidos platônicos eram associados pelos gregos aos quatro elementos clássicos: o cubo à terra, o tetraedro ao fogo, o octaedro ao ar e o icosaedro à água. O dodecaedro era associado ao universo, o que mostra a importância que davam a essas formas geométricas.
Aplicações dos Poliedros
**Logo**, os poliedros não são apenas objetos de estudo teórico. **Em resumo**, eles possuem aplicações práticas em diversas áreas:
- Arquitetura: **Inegavelmente**, as formas dos poliedros são usadas na construção de edifícios e estruturas, como cúpulas geodésicas e outras construções. **Por exemplo**, o Museu do Amanhã no Rio de Janeiro, tem partes de sua estrutura baseadas em poliedros.
- Cristalografia: **Da mesma forma**, os poliedros são utilizados para descrever as formas de cristais encontrados na natureza. **A saber**, cada tipo de cristal possui uma forma poliedrica característica.
- Design de jogos: **Assim também**, formas de poliedros são usadas na criação de dados de RPG, objetos virtuais e cenários em jogos. **Para ilustrar**, as formas de dados de jogos são baseados em poliedros como o cubo e o dodecaedro.
- Biologia: **De fato**, as estruturas de certos vírus e outras partículas biológicas assemelham-se a poliedros. **Por exemplo**, muitos vírus têm a forma de icosaedros.
- Química: **Assim como**, as estruturas moleculares de muitos compostos seguem padrões poliedricos. **Nesse sentido**, a geometria molecular de alguns compostos é influenciada por poliedros.
Exercícios Resolvidos
1. Um poliedro convexo possui 12 vértices e 18 arestas. Quantas faces ele tem?
Resposta: Para resolver, usamos a relação de Euler: V – A + F = 2. Substituindo V = 12 e A = 18, temos:
Portanto, o poliedro tem 8 faces.
2. Um poliedro convexo possui 20 faces triangulares. Quantas arestas ele tem?
Resposta: Cada face triangular tem 3 arestas, mas cada aresta é compartilhada por duas faces. Então o número total de arestas é:
Portanto, o poliedro tem 30 arestas.
3. Quantos vértices possui um cubo?
Resposta: Um cubo possui 8 vértices. Cada um dos cantos do cubo é um vértice.
4. Qual dos seguintes poliedros é um poliedro de Platão?
- Prisma
- Pirâmide
- Dodecaedro
- Cubo truncado
- Bipirâmide
Resposta: A alternativa correta é a letra “c”. Os poliedros de Platão são: tetraedro, cubo (hexaedro), octaedro, dodecaedro e icosaedro.
Exercícios Propostos
5. Um poliedro convexo possui 6 faces quadradas e 8 faces triangulares. Quantos vértices esse poliedro tem?
- 12
- 18
- 20
- 24
- 30
Resposta: A alternativa correta é a letra “a”.
Resolução: Primeiro, encontre o número total de arestas: (6 * 4 + 8 * 3) / 2 = (24 + 24) / 2 = 24. Depois, use a relação de Euler: V – A + F = 2. Substituindo os valores: V – 24 + (6+8) = 2, V – 24 + 14 = 2, V – 10 = 2, V = 12.
6. Um poliedro possui 10 faces, sendo 8 triângulos e 2 pentágonos. Quantas arestas ele tem?
- 15
- 20
- 25
- 30
- 35
Resposta: A alternativa correta é a letra “c”.
Resolução: Calcule o total de arestas: (8 * 3 + 2 * 5) / 2 = (24 + 10) / 2 = 34 / 2 = 17.
7. Qual a quantidade de faces, vértices e arestas de um icosaedro?
- F=12, V=20, A=30
- F=20, V=12, A=30
- F=20, V=30, A=12
- F=30, V=12, A=20
- F=12, V=30, A=20
Resposta: A alternativa correta é a letra “b”.
Resolução: Um icosaedro possui 20 faces, 12 vértices e 30 arestas.
8. Se um poliedro tem 20 faces e 30 arestas, quantos vértices ele tem?
- 10
- 12
- 14
- 15
- 16
Resposta: A alternativa correta é a letra “b”.
Resolução: Utilize a relação de Euler: V – A + F = 2. Substituindo os valores V – 30 + 20 = 2, V – 10 = 2, V = 12.
**Em suma**, os poliedros são figuras geométricas fascinantes que se manifestam em muitas formas ao nosso redor. **Portanto**, esperamos que este guia tenha esclarecido os principais conceitos e instigado seu interesse por este tema. **Finalmente**, convido você a continuar explorando a beleza da matemática!
Para complementar seus estudos, você pode conferir nossos artigos sobre Retas Perpendiculares e Razões Trigonométricas no Triângulo Retângulo, onde você poderá explorar mais sobre geometria!
**Não perca a oportunidade de aprender mais!** Inscreva-se agora em nosso canal no YouTube e descubra vídeos incríveis sobre matemática: Matexpl. **Junte-se à nossa comunidade e vamos desvendar os mistérios da matemática juntos!**
Este artigo foi desenvolvido com o objetivo de oferecer uma visão geral dos poliedros, combinando teoria, exemplos práticos e aplicações relevantes. Esperamos que tenha sido útil e inspirador.

Deixe um comentário