Matemática Explorada

Certamente, ao adentrar no mundo da geometria plana, nos deparamos com conceitos que são a base para compreender as relações entre figuras e suas propriedades. Assim sendo, as retas paralelas e transversais são elementos fundamentais nesse estudo. Afinal, entender o que são e como interagem, é essencial para construir conhecimentos sólidos em geometria, além disso, esse conhecimento é muito útil para o dia a dia. Neste artigo, vamos explorar esses conceitos em detalhes, incluindo definições, ângulos formados, exemplos práticos e exercícios para fixação do conteúdo.

A princípio, vamos começar com as definições básicas de retas paralelas e transversais. Similarmente, ao longo do artigo, vamos analisar diversos exemplos práticos e aplicações, tudo de uma forma didática e clara, como um verdadeiro livro didático.

O que são Retas Paralelas e Transversais?

Retas paralelas são aquelas que se encontram no mesmo plano e nunca se cruzam, ou seja, elas mantêm sempre a mesma distância entre si. Por outro lado, uma reta transversal é aquela que intercepta duas ou mais retas paralelas. Dessa forma, ao fazer essa intersecção, a reta transversal cria ângulos que possuem características e propriedades muito importantes, que iremos estudar a seguir.

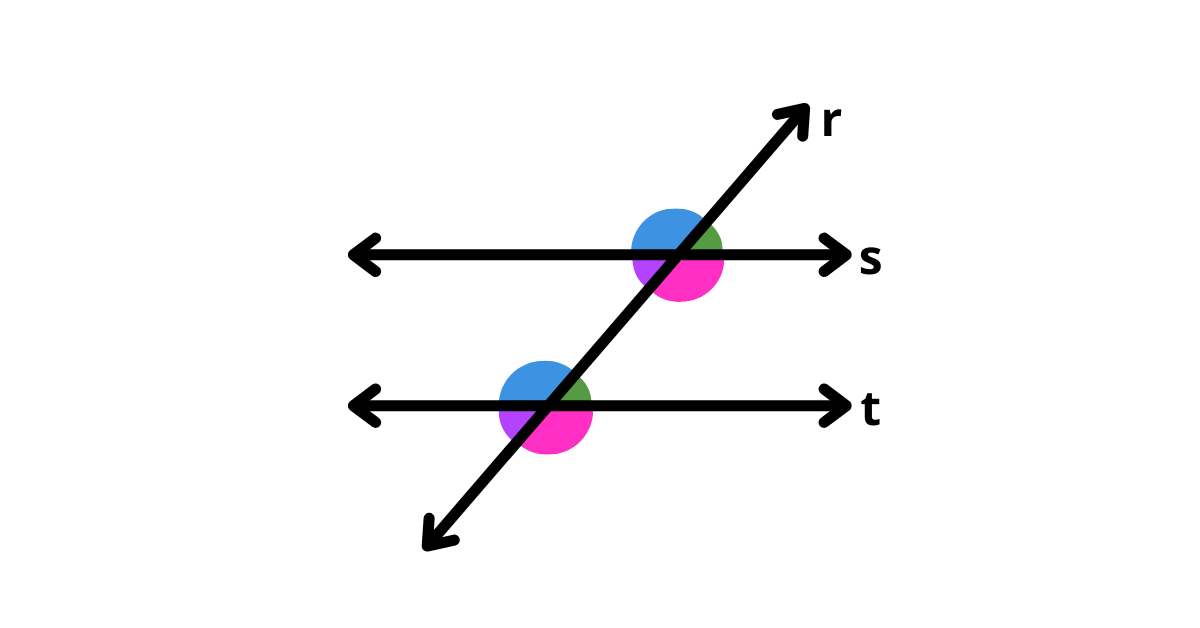
Representação de retas paralelas e uma transversal.

Ângulos Formados por Retas Paralelas e Transversais

Quando uma reta transversal intercepta duas retas paralelas, diversos ângulos são formados, sendo eles:

• Ângulos Correspondentes: São ângulos que ocupam a mesma posição em relação às retas paralelas e à transversal. Ou seja, eles possuem medidas iguais.
• Ângulos Alternos Internos: São ângulos que estão entre as retas paralelas e em lados opostos da transversal. Analogamente, eles possuem medidas iguais.
• Ângulos Alternos Externos: São ângulos que estão fora das retas paralelas e em lados opostos da transversal. Assim como os alternos internos, eles também possuem medidas iguais.
• Ângulos Colaterais Internos: São ângulos que estão entre as retas paralelas e no mesmo lado da transversal. Em contrapartida, eles são suplementares, ou seja, a soma de suas medidas é 180°.
• Ângulos Colaterais Externos: São ângulos que estão fora das retas paralelas e no mesmo lado da transversal. Semelhantemente, eles também são suplementares.

Nesse sentido, compreender essas relações entre os ângulos formados pelas retas paralelas e transversais é fundamental para resolver diversos problemas de geometria, e também para entender o mundo que nos cerca.

Aplicações Práticas e a Importância nos Estudos

A saber, retas paralelas e transversais não são apenas conceitos abstratos da geometria, mas ferramentas poderosas que estão presentes em diversas situações do nosso cotidiano. Diga-se de passagem, observe alguns exemplos:

• Arquitetura: Em construções, as linhas paralelas são usadas para projetar paredes, pisos, vigas e outras estruturas.
• Urbanismo: No planejamento urbano, o conceito de paralelas e transversais é usado para definir o traçado de ruas e avenidas.
• Design Gráfico: No design gráfico, os conceitos de paralelas e transversais são muito usados para criar diagramas, layouts, e ilustrações.
• Música: Até mesmo na música, as pautas (conjunto de cinco linhas paralelas) utilizam o conceito de retas paralelas.
• Mosaicos: Na arte, os mosaicos utilizam o conceito de retas paralelas e transversais para criar padrões e formas.

Em suma, o entendimento das propriedades das retas paralelas e transversais é, sem dúvida, essencial para diversas áreas profissionais, e para a compreensão de outros temas da geometria e da matemática. Além disso, é um tópico comum em provas de concursos e vestibulares, por isso, se prepare e continue estudando.

Um Breve Histórico: Os Matemáticos que Exploraram as Retas

Aliás, o estudo das retas paralelas e transversais não é recente. A saber, matemáticos da antiguidade como Euclides, já estudava sobre retas e geometria, sendo que o seu trabalho influenciou a matemática por vários séculos. Contudo, outros matemáticos contribuíram para o refinamento do conhecimento sobre retas paralelas, incluindo seus ângulos e propriedades. Portanto, é importante reconhecer a importância do trabalho desses gênios, que nos permitiram compreender as relações espaciais e geométricas com mais profundidade.

Exercícios Resolvidos: Passo a Passo

A fim de praticar o que foi aprendido, vamos resolver alguns exercícios juntos. Preste bastante atenção e tente entender cada etapa!

Exercícios Propostos: Teste Seus Conhecimentos

Agora, chegou a sua vez! Resolva os exercícios abaixo e, em seguida, compare suas respostas com a resolução passo a passo. Lembre-se, o mais importante é tentar e aprender com seus erros!

Se, porventura, você queira explorar mais este tema, não deixe de conferir este vídeo incrível do nosso canal: Vídeos sobre Geometria no Matemática Explorada, onde explicamos em detalhes vários assuntos sobre geometria. Similarmente, você também pode explorar outros assuntos relacionados como razões trigonométricas no triângulo retângulo aqui no nosso site.

Conclusão

Finalmente, o estudo das retas paralelas e transversais é, sem dúvida, essencial para compreender diversas relações na geometria plana e no nosso cotidiano. Afinal, a compreensão desses conceitos permitirá que você avance nos estudos da geometria e aplique esse conhecimento em diversas situações. Ou seja, continue estudando e explorando os fascinantes mistérios da matemática!