Primeiramente, vamos iniciar nossa jornada na matemática com uma introdução a matrizes, um conceito fundamental. Afinal, matrizes são ferramentas poderosas que nos permitem organizar e manipular dados de forma eficiente. Sobretudo, elas estão presentes em diversas áreas, desde a computação gráfica até a resolução de sistemas lineares. Portanto, entender o que são matrizes e como elas funcionam é essencial para qualquer estudante de matemática, engenharia, ciência da computação, ou áreas relacionadas. Assim sendo, este artigo é o ponto de partida para aprofundarmos nossos conhecimentos nesse tema fascinante.
O Que São Matrizes? (Definição e Motivação)
Em princípio, uma matriz é uma tabela retangular de números, símbolos ou expressões, organizadas em linhas e colunas. Analogamente, pense em uma planilha eletrônica: as células são preenchidas com valores, que formam linhas e colunas. Aliás, essa analogia é muito útil para compreendermos a essência de uma matriz. Dessa forma, ela nos permite armazenar e organizar dados de forma estruturada, facilitando a sua manipulação e análise. Ademais, a organização dos elementos em linhas e colunas permite que possamos trabalhar com os dados de maneira mais eficiente. Inclusive, muitas vezes, podemos representar um problema do mundo real através de uma matriz.
Por exemplo, imagine uma tabela de preços em um supermercado. Nesse sentido, cada linha representa um produto, e cada coluna representa o preço em um dia da semana. De fato, essa tabela é uma matriz! Outrossim, podemos usar matrizes para representar notas de alunos em diferentes disciplinas, os resultados de uma pesquisa, ou até mesmo os pixels de uma imagem. Nesse sentido, as matrizes são uma maneira eficiente de organizar dados e realizar diversas operações matemáticas sobre eles.
A saber, matrizes não são apenas um amontoado de números. Pelo contrário, elas têm uma estrutura muito bem definida, e é justamente essa estrutura que nos permite realizar cálculos complexos e resolver problemas práticos. Por exemplo, em computação gráfica, matrizes são usadas para transformar imagens, movê-las, rotacioná-las e dimensioná-las. Em outras palavras, as matrizes são a base de muitos algoritmos gráficos que usamos diariamente. Assim, elas tornam-se essenciais para diversas áreas.
De acordo com o matemático inglês Arthur Cayley, um dos pioneiros no estudo das matrizes, esse conceito tem aplicações muito além da matemática pura. Nesse sentido, Cayley introduziu as matrizes em 1858, no seu artigo “A memoir on the theory of matrices”, como uma ferramenta para auxiliar na resolução de sistemas de equações lineares. Consequentemente, o conceito revolucionou a matemática e sua aplicação em outros campos da ciência.
Representação Gráfica e Notação Básica
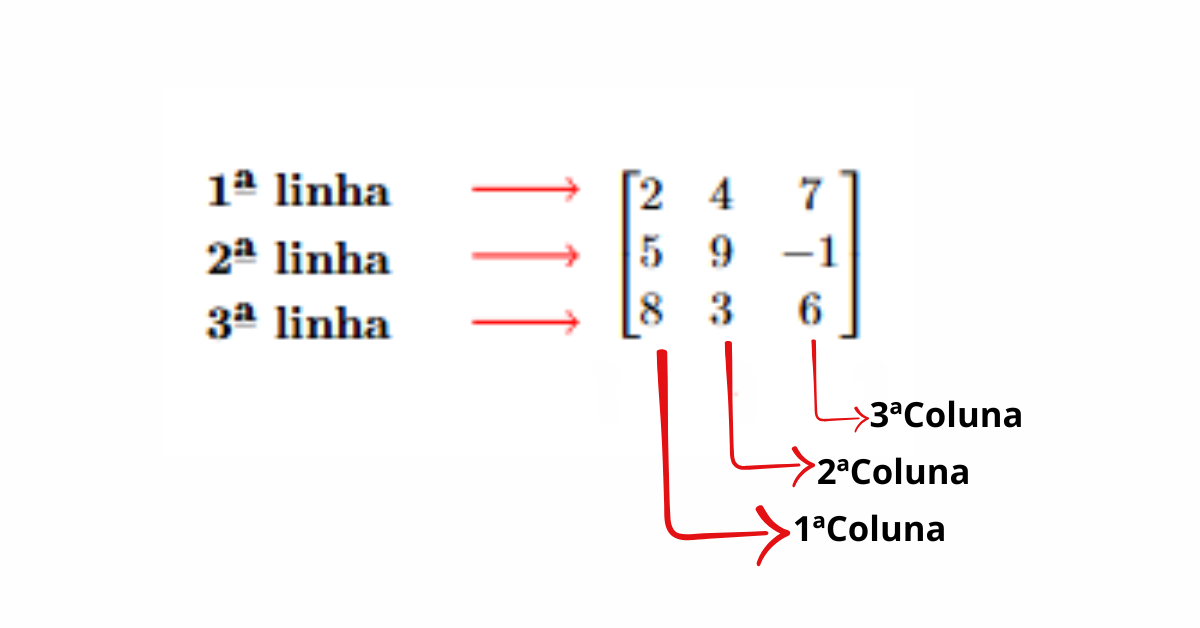
Agora que entendemos o que são matrizes, é preciso aprender como representá-las e nomeá-las. Geralmente, usamos letras maiúsculas para representar matrizes, como A, B, C, etc. Além disso, os elementos de uma matriz são geralmente representados por letras minúsculas com dois índices, como aij. Dessa forma, o primeiro índice ‘i’ indica a linha em que o elemento está, e o segundo índice ‘j’ indica a coluna. Por exemplo, a23 é o elemento que está na segunda linha e terceira coluna da matriz A.
Usualmente, as matrizes são representadas entre colchetes ou parênteses. Por exemplo, uma matriz A de ordem 2×3 (2 linhas e 3 colunas) pode ser escrita como:
\[ A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix} \]
Nesse ínterim, a ordem da matriz, também chamada de dimensão da matriz, é um conceito fundamental. Assim sendo, ela é indicada pelo número de linhas e colunas da matriz, nessa ordem. Por exemplo, uma matriz de ordem 3×4 tem 3 linhas e 4 colunas. Por conseguinte, matrizes com ordens diferentes são consideradas matrizes diferentes, ainda que tenham os mesmos elementos.
Conforme podemos observar, a representação gráfica de uma matriz é bem simples e intuitiva, sendo que inclusive essa notação padronizada é fundamental para podermos comunicar as informações de maneira precisa e evitar ambiguidades. Atualmente, muitos softwares e ferramentas de programação utilizam essa mesma notação. Eventualmente, podemos usar essa notação para descrever matrizes em diferentes contextos matemáticos e computacionais.
Exemplo Prático
Só para ilustrar, considere a seguinte matriz B:
\[ B = \begin{bmatrix} 5 & 2 & 7 \\ 1 & 9 & 4 \end{bmatrix} \]
Nesse caso, a matriz B tem 2 linhas e 3 colunas, ou seja, é uma matriz de ordem 2×3. Assim como no exemplo acima, o elemento b11 é 5, o elemento b12 é 2 e o elemento b23 é 4. De modo que, cada elemento é identificado por sua posição dentro da matriz, o que nos permite acessá-lo de forma eficiente.
Elementos de uma Matriz
Como já vimos, os elementos de uma matriz são os valores que a compõem, organizados em linhas e colunas. Em resumo, os elementos podem ser números, símbolos ou expressões matemáticas. A saber, cada elemento é identificado por sua posição na matriz, ou seja, sua linha e coluna. Dessa maneira, a notação aij indica o elemento que está na linha i e coluna j da matriz A.
Por exemplo, na matriz B mostrada anteriormente, o elemento b21 (segunda linha e primeira coluna) é 1, e o elemento b13 (primeira linha e terceira coluna) é 7. Portanto, é muito importante saber localizar os elementos dentro de uma matriz, pois as operações matemáticas realizadas com matrizes dependem diretamente dessa localização. Por conseguinte, os elementos são os blocos fundamentais com os quais podemos manipular matrizes.
Contudo, é fundamental ter em mente que a ordem de linhas e colunas é sempre a mesma. Ou seja, primeiro a linha e depois a coluna. Assim, a notação aij é universal e a ordem na qual escrevemos os índices i e j tem muita importância. De acordo com isso, devemos sempre ter atenção quando estamos manipulando matrizes para não confundir linhas com colunas.
Exemplo Ilustrativo
Para ilustrar melhor, vamos considerar a matriz C a seguir:
\[ C = \begin{bmatrix} 10 & 20 & 30 & 40\\ 50 & 60 & 70 & 80\\ 90 & 100 & 110 & 120 \end{bmatrix} \]
Nesse sentido, a matriz C tem ordem 3×4. Então, podemos identificar seus elementos da seguinte forma: o elemento c11 é 10, o elemento c23 é 70 e o elemento c34 é 120. Isto é, cada elemento tem um endereço único na matriz, determinado pela sua linha e coluna. Logo, essa organização nos permite trabalhar com os dados de forma precisa e eficiente.
Exercícios de Fixação
Agora que já aprendemos o básico sobre matrizes, é hora de praticar com alguns exercícios. Dessa forma, vamos fixar os conceitos que abordamos até aqui. Assim sendo, tente resolver cada questão e em seguida confira as respostas.
1. Qual é a ordem da matriz abaixo?
\[ A = \begin{bmatrix} 2 & 4 & 6 \\ 1 & 3 & 5 \end{bmatrix} \]
Resposta: c) 2×3
Explicação: A matriz possui 2 linhas e 3 colunas, portanto, sua ordem é 2×3.
2. Dada a matriz abaixo, qual o valor do elemento a21?
\[ B = \begin{bmatrix} 7 & 8 & 9 \\ 4 & 5 & 6 \\ 1 & 2 & 3 \end{bmatrix} \]
Resposta: b) 4
Explicação: O elemento a21 está na segunda linha e primeira coluna, logo o valor é 4.
3. Dada a matriz abaixo, qual o valor do elemento c32?
\[ C = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ 7 & 8 \end{bmatrix} \]
Resposta: b) 6
Explicação: O elemento c32 está na terceira linha e segunda coluna, desse modo o valor é 6.
4. Qual a ordem da matriz abaixo?
\[ D = \begin{bmatrix} 1 & 2 & 3 & 4 \end{bmatrix} \]
Resposta: a) 1×4
Explicação: A matriz possui 1 linha e 4 colunas, logo, sua ordem é 1×4.
5. Dada a matriz abaixo, qual o valor do elemento e13?
\[ E = \begin{bmatrix} 9 & 10 & 11 \\ 12 & 13 & 14 \end{bmatrix} \]
Resposta: a) 11
Explicação: O elemento e13 está na primeira linha e terceira coluna, então o valor é 11.
6. Qual é a ordem da matriz F abaixo?
\[ F = \begin{bmatrix} 8 \\ 16 \\ 24 \end{bmatrix} \]
Resposta: b) 3×1
Explicação: A matriz possui 3 linhas e 1 coluna, assim sua ordem é 3×1.
7. Dada a matriz abaixo, qual o valor do elemento g42?
\[ G = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ 10 & 11 & 12 \end{bmatrix} \]
Resposta: a) 11
Explicação: O elemento g42 está na quarta linha e segunda coluna, entretanto o valor é 11.
8. Qual a ordem da matriz H abaixo?
\[ H = \begin{bmatrix} 13 & 14 \\ 15 & 16 \\ 17 & 18 \end{bmatrix} \]
Resposta: b) 3×2
Explicação: A matriz possui 3 linhas e 2 colunas, portanto sua ordem é 3×2.
Conclusão
Em suma, neste artigo exploramos a introdução a matrizes, seu conceito fundamental, sua notação e como identificar seus elementos. Desse modo, você deu o primeiro passo para entender essa ferramenta poderosa da matemática. Além disso, vimos que matrizes são tabelas retangulares de números, símbolos ou expressões, organizadas em linhas e colunas. Posteriormente, aprendemos como representar matrizes usando colchetes ou parênteses e a notação aij para identificar os elementos. Finalmente, praticamos com exercícios para fixar os conceitos. Entretanto, ainda temos muito a aprender sobre matrizes. Assim sendo, no próximo artigo, vamos explorar os tipos de matrizes e suas aplicações práticas. Logo, continue conosco nessa jornada e descubra o mundo das matrizes!
Se você gostou deste artigo e quer aprender mais sobre outros temas da matemática, visite nosso guia completo sobre Progressão Aritmética. Ainda mais, para complementar seus estudos, não deixe de conferir nosso canal no YouTube, Matemática Explorada, onde você encontrará vídeos com explicações e exercícios sobre diversos assuntos da matemática.

Deixe um comentário