Anteriormente, exploramos cada uma das operações básicas com matrizes: adição, subtração e multiplicação por escalar. Agora, vamos dar um passo adiante e combinar essas operações em uma mesma expressão. Afinal, na matemática, muitas vezes, precisamos utilizar diversas operações em sequência para resolver um problema. Nesse sentido, neste artigo, vamos aprender como combinar essas operações com matrizes, seguindo as regras da matemática e a ordem correta. Portanto, este artigo tem como objetivo apresentar exemplos práticos e exercícios para você se familiarizar com as operações combinadas e consolidar seu aprendizado.
Revisão das Operações Básicas
Inicialmente, vamos relembrar rapidamente as operações que já estudamos. Assim sendo, a adição de matrizes consiste em somar os elementos correspondentes de matrizes de mesma ordem. Analogamente, a subtração consiste em subtrair os elementos correspondentes de matrizes de mesma ordem. Já a multiplicação de matriz por escalar consiste em multiplicar cada elemento da matriz por um número, chamado escalar. Em resumo, essas são as três operações básicas que usaremos para construir as expressões mais complexas que veremos neste artigo. Dessa forma, ter um bom domínio dessas operações é fundamental para que possamos combiná-las e realizar cálculos mais complexos.
Contudo, é importante ressaltar que, nas operações combinadas, a ordem em que as operações são realizadas é muito importante. Ou seja, assim como na matemática tradicional, a multiplicação por escalar deve ser realizada antes da adição e subtração, a menos que os parênteses indiquem o contrário. Por conseguinte, essa ordem é fundamental para garantir que o resultado final esteja correto. Portanto, a atenção à ordem das operações é crucial para a resolução de exercícios que envolvem operações combinadas com matrizes.
Ordem das Operações
Como já mencionado, a ordem das operações em expressões com matrizes segue os mesmos princípios da matemática tradicional. A saber, primeiro realizamos as multiplicações por escalar e depois as adições e subtrações, sempre da esquerda para a direita. Por exemplo, em uma expressão do tipo k * A + B, primeiro multiplicamos a matriz A pelo escalar k e depois adicionamos o resultado à matriz B. Desse modo, essa ordem garante a coerência e a unicidade do resultado.
Para ilustrar melhor, vamos analisar um exemplo prático. Suponha que temos as matrizes A e B e o escalar k = 2:
\[ A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \] \[ B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} \]
Então, para calcular a matriz resultante C = 2 * A + B, seguimos a seguinte ordem:
- Primeiro, multiplicamos a matriz A pelo escalar 2: \[2 \cdot A = 2 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix}\]
- Em seguida, somamos o resultado à matriz B: \[ \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix} + \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 2+5 & 4+6 \\ 6+7 & 8+8 \end{bmatrix} = \begin{bmatrix} 7 & 10 \\ 13 & 16 \end{bmatrix}\]
Portanto, o resultado da expressão 2 * A + B é a matriz C = \[ \begin{bmatrix} 7 & 10 \\ 13 & 16 \end{bmatrix} \] . Como podemos ver, a ordem das operações é crucial para chegarmos ao resultado correto.
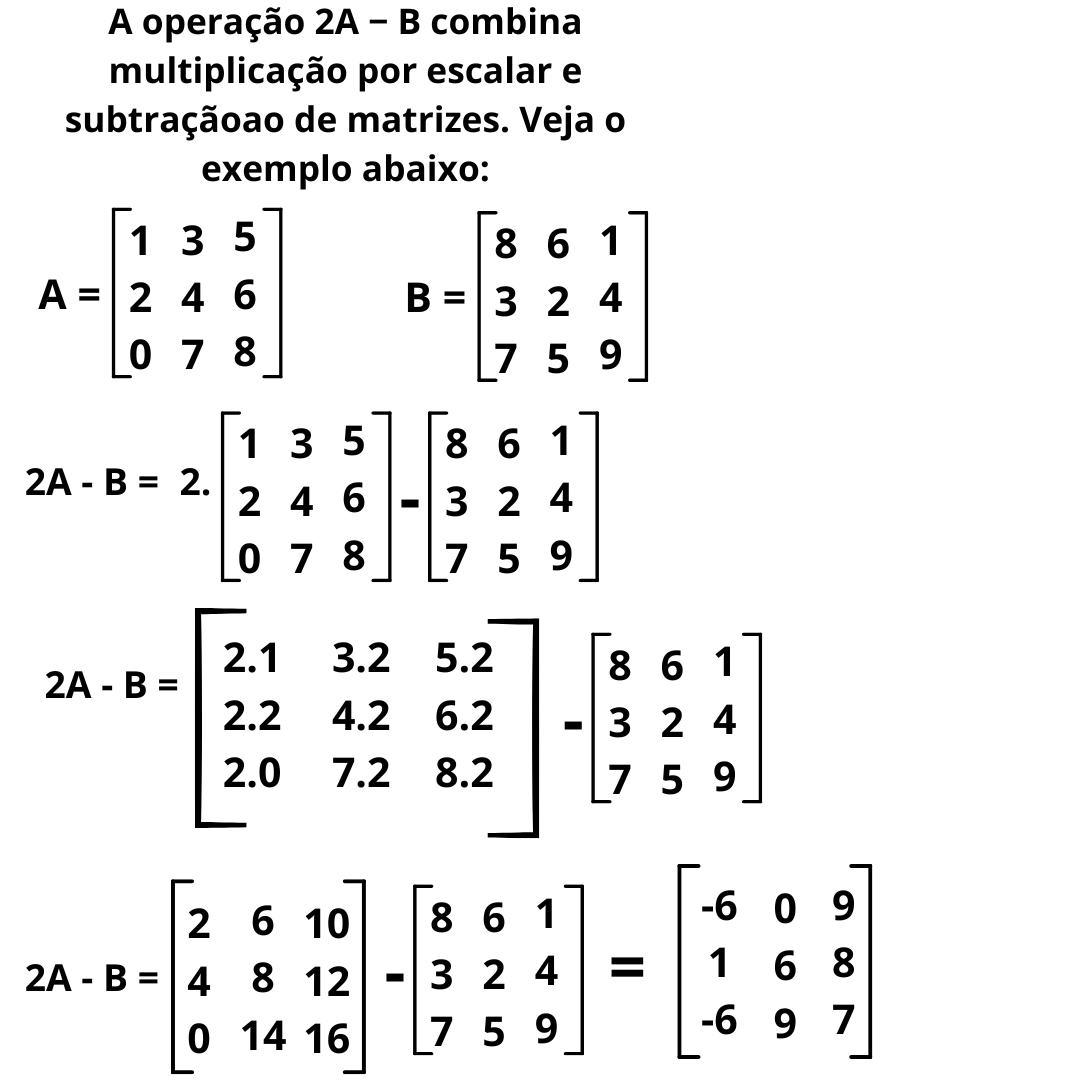
Exemplos Práticos com Operações Combinadas
Agora que entendemos a ordem das operações, vamos explorar exemplos práticos que combinam adição, subtração e multiplicação por escalar. Assim sendo, vamos analisar diversos casos para que você possa consolidar o seu aprendizado. Lembre-se, sempre que a multiplicação por escalar é realizada antes da adição ou subtração.
Exemplo 1: Combinação com Duas Multiplicações por Escalar
Suponha que temos as matrizes A e B e os escalares k = 2 e m = -1:
\[ A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \] \[ B = \begin{bmatrix} 5 & -1 \\ 2 & 3 \end{bmatrix} \]
Então, para calcular a matriz resultante C = k * A + m * B, seguimos a seguinte ordem:
- Multiplicamos a matriz A por k = 2: \[2 \cdot A = 2 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix}\]
- Multiplicamos a matriz B por m = -1: \[-1 \cdot B = -1 \cdot \begin{bmatrix} 5 & -1 \\ 2 & 3 \end{bmatrix} = \begin{bmatrix} -5 & 1 \\ -2 & -3 \end{bmatrix}\]
- Somamos os resultados: \[ \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix} + \begin{bmatrix} -5 & 1 \\ -2 & -3 \end{bmatrix} = \begin{bmatrix} 2-5 & 4+1 \\ 6-2 & 8-3 \end{bmatrix} = \begin{bmatrix} -3 & 5 \\ 4 & 5 \end{bmatrix}\]
Nesse caso, o resultado final é a matriz C = \[ \begin{bmatrix} -3 & 5 \\ 4 & 5 \end{bmatrix} \] . Como você pode observar, realizamos todas as multiplicações por escalar antes da adição.
Exemplo 2: Combinação com Subtração e Multiplicação
Agora, vamos considerar uma combinação com subtração e multiplicação por escalar. Suponha que temos as matrizes D e E e o escalar k = 3:
\[ D = \begin{bmatrix} 4 & 5 \\ 1 & 2 \end{bmatrix} \] \[ E = \begin{bmatrix} 2 & 0 \\ -1 & 3 \end{bmatrix} \]
Então, para calcular a matriz resultante F = D – 3 * E, seguimos a seguinte ordem:
- Multiplicamos a matriz E por k = 3: \[3 \cdot E = 3 \cdot \begin{bmatrix} 2 & 0 \\ -1 & 3 \end{bmatrix} = \begin{bmatrix} 6 & 0 \\ -3 & 9 \end{bmatrix}\]
- Subtraímos o resultado da matriz D: \[\begin{bmatrix} 4 & 5 \\ 1 & 2 \end{bmatrix} – \begin{bmatrix} 6 & 0 \\ -3 & 9 \end{bmatrix} = \begin{bmatrix} 4-6 & 5-0 \\ 1-(-3) & 2-9 \end{bmatrix} = \begin{bmatrix} -2 & 5 \\ 4 & -7 \end{bmatrix}\]
Portanto, o resultado final é a matriz F = \[ \begin{bmatrix} -2 & 5 \\ 4 & -7 \end{bmatrix} \] . Note que a subtração é realizada após a multiplicação.
Resolvendo Problemas com Operações Combinadas
Agora que já entendemos como combinar as operações com matrizes, vamos analisar como usar essas operações para resolver problemas mais complexos. Assim, vamos praticar com exemplos que exigem um pouco mais de raciocínio lógico e atenção. Por conseguinte, vamos explorar diferentes tipos de problemas, incluindo a determinação de matrizes desconhecidas em uma expressão.
Por exemplo, vamos determinar o valor da matriz X na seguinte expressão: 2X + A = B, onde A = \[ \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \] e B = \[ \begin{bmatrix} 7 & 8 \\ 9 & 10 \end{bmatrix} \] . Para resolver, seguimos os seguintes passos:
- Isolamos 2X: 2X = B – A
- Calculamos B – A: \[\begin{bmatrix} 7 & 8 \\ 9 & 10 \end{bmatrix} – \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 6 & 6 \\ 6 & 6 \end{bmatrix}\]
- Multiplicamos ambos os lados da equação por 1/2: X = (1/2)(B – A)
- Calculamos (1/2)(B – A): \[\frac{1}{2} \cdot \begin{bmatrix} 6 & 6 \\ 6 & 6 \end{bmatrix} = \begin{bmatrix} 3 & 3 \\ 3 & 3 \end{bmatrix}\]
Portanto, a matriz X é igual a \[ \begin{bmatrix} 3 & 3 \\ 3 & 3 \end{bmatrix} \]. Como você pode observar, a resolução de problemas que envolvem matrizes requer um bom entendimento da ordem das operações e do processo de manipulação das matrizes.
Exercícios de Fixação (Combinando Operações)
Agora, vamos praticar com exercícios que combinam as três operações (adição, subtração e multiplicação por escalar). Assim sendo, resolva as questões abaixo e logo após confira as respostas passo a passo.
1. Calcule a matriz resultante de 2A + B, sabendo que:
\[ A = \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix} \] \[ B = \begin{bmatrix} 3 & 1 \\ 2 & 0 \end{bmatrix} \]
Resposta: a) \[ \begin{bmatrix} 5 & 5 \\ 2 & 2 \end{bmatrix} \]
Explicação: Primeiro, 2A = \[ \begin{bmatrix} 2 & 4 \\ 0 & 2 \end{bmatrix} \]. Em seguida, 2A + B = \[ \begin{bmatrix} 2+3 & 4+1 \\ 0+2 & 2+0 \end{bmatrix} = \begin{bmatrix} 5 & 5 \\ 2 & 2 \end{bmatrix} \]
2. Sendo A = \[ \begin{bmatrix} 3 & 1 \\ 2 & -1 \end{bmatrix} \] e B = \[ \begin{bmatrix} 1 & 0 \\ -2 & 3 \end{bmatrix} \], calcule A – 2B:
Resposta: a) \[ \begin{bmatrix} 1 & 1 \\ 6 & -7 \end{bmatrix} \]
Explicação: Primeiro, 2B = \[ \begin{bmatrix} 2 & 0 \\ -4 & 6 \end{bmatrix} \]. Em seguida, A – 2B = \[ \begin{bmatrix} 3-2 & 1-0 \\ 2-(-4) & -1-6 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 6 & -7 \end{bmatrix} \]
3. Se C = \[ \begin{bmatrix} 5 & 0 \\ 2 & 1 \\ 3 & 4 \end{bmatrix} \] e D = \[ \begin{bmatrix} 1 & 2 \\ 0 & -1 \\ -2 & 0 \end{bmatrix} \], calcule 3C – D:
Resposta: a) \[ \begin{bmatrix} 14 & -2 \\ 6 & 4 \\ 11 & 12 \end{bmatrix} \]
Explicação: Primeiro, 3C = \[ \begin{bmatrix} 15 & 0 \\ 6 & 3 \\ 9 & 12 \end{bmatrix} \]. Em seguida, 3C – D = \[\begin{bmatrix} 15-1 & 0-2 \\ 6-0 & 3-(-1) \\ 9-(-2) & 12-0 \end{bmatrix} = \begin{bmatrix} 14 & -2 \\ 6 & 4 \\ 11 & 12 \end{bmatrix} \]
4. Se E = \[ \begin{bmatrix} 0 & 1 \\ -1 & 2 \end{bmatrix} \] e F = \[ \begin{bmatrix} 2 & 3 \\ -2 & 0 \end{bmatrix} \], determine 2E + 3F:
Resposta: a) \[ \begin{bmatrix} 6 & 11 \\ -8 & 4 \end{bmatrix} \]
Explicação: Primeiro, 2E = \[ \begin{bmatrix} 0 & 2 \\ -2 & 4 \end{bmatrix} \] e 3F = \[ \begin{bmatrix} 6 & 9 \\ -6 & 0 \end{bmatrix} \]. Em seguida, 2E + 3F = \[ \begin{bmatrix} 0+6 & 2+9 \\ -2-6 & 4+0 \end{bmatrix} = \begin{bmatrix} 6 & 11 \\ -8 & 4 \end{bmatrix} \]
5. Sendo A = \[ \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix} \] , calcule 2A – A:
Resposta: a) \[ \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix} \]
Explicação: Primeiro, 2A = \[ \begin{bmatrix} 2 & 0 & 2 \\ 0 & 2 & 0 \\ 2 & 0 & 2 \end{bmatrix} \]. Em seguida, 2A – A = \[ \begin{bmatrix} 2-1 & 0-0 & 2-1 \\ 0-0 & 2-1 & 0-0 \\ 2-1 & 0-0 & 2-1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix} \]
6. Se C = \[ \begin{bmatrix} 2 & -1 \\ 0 & 3 \end{bmatrix} \] e D = \[ \begin{bmatrix} -1 & 2 \\ 1 & 0 \end{bmatrix} \], encontre 2C – 3D:
Resposta: a) \[ \begin{bmatrix} 7 & -8 \\ -3 & 6 \end{bmatrix} \]
Explicação: Primeiro, 2C = \[ \begin{bmatrix} 4 & -2 \\ 0 & 6 \end{bmatrix} \] e 3D = \[ \begin{bmatrix} -3 & 6 \\ 3 & 0 \end{bmatrix} \]. Em seguida, 2C – 3D = \[ \begin{bmatrix} 4-(-3) & -2-6 \\ 0-3 & 6-0 \end{bmatrix} = \begin{bmatrix} 7 & -8 \\ -3 & 6 \end{bmatrix} \]
7. Calcule o valor da matriz X na expressão: 2X + \[ \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \] = \[ \begin{bmatrix} 7 & 8 \\ 9 & 10 \end{bmatrix} \] :
Resposta: a) \[ \begin{bmatrix} 3 & 3 \\ 3 & 3 \end{bmatrix} \]
Explicação: Primeiro, isolamos 2X = \[ \begin{bmatrix} 7 & 8 \\ 9 & 10 \end{bmatrix} \] – \[ \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \] = \[ \begin{bmatrix} 6 & 6 \\ 6 & 6 \end{bmatrix} \] . Em seguida, X = (1/2) \[ \begin{bmatrix} 6 & 6 \\ 6 & 6 \end{bmatrix} \] = \[ \begin{bmatrix} 3 & 3 \\ 3 & 3 \end{bmatrix} \]
8. Se M = \[ \begin{bmatrix} 2 & 1 \\ 0 & -1 \end{bmatrix} \] e N = \[ \begin{bmatrix} 1 & 0 \\ 2 & 3 \end{bmatrix} \], encontre 2M + (1/2)N:
Resposta: c) \[ \begin{bmatrix} 4.5 & 2 \\ 1 & -0.5 \end{bmatrix} \]
Explicação: Primeiro, 2M = \[ \begin{bmatrix} 4 & 2 \\ 0 & -2 \end{bmatrix} \] e (1/2)N = \[ \begin{bmatrix} 0.5 & 0 \\ 1 & 1.5 \end{bmatrix} \]. Em seguida, 2M + (1/2)N = \[ \begin{bmatrix} 4+0.5 & 2+0 \\ 0+1 & -2+1.5 \end{bmatrix} = \begin{bmatrix} 4.5 & 2 \\ 1 & -0.5 \end{bmatrix} \]
Conclusão
Em suma, neste artigo, exploramos as operações combinadas com matrizes, que envolvem a adição, subtração e multiplicação por escalar. Vimos que a ordem das operações é crucial para se obter o resultado correto, sendo que a multiplicação por escalar tem prioridade em relação à adição e subtração. Ademais, praticamos com diversos exemplos e exercícios para que você possa consolidar seu aprendizado. Portanto, agora você está apto a resolver expressões mais complexas envolvendo matrizes. Assim sendo, no próximo artigo, vamos explorar uma operação mais complexa e fundamental: a multiplicação entre matrizes. Logo, continue nos acompanhando nesta jornada no mundo da álgebra linear! Para aprofundar seus conhecimentos, explore nosso artigo sobre Tipos de Matrizes e

Deixe um comentário