Primordialmente, a fundamental sequência matemática conhecida como Progressão Aritmética, amplamente reconhecida como P.A., constitui um conceito matemático avançado que influencia diversos cálculos sequenciais no cotidiano educacional. De fato, esta didática sequência numérica especial desperta imenso interesse acadêmico devido à sua extensa aplicabilidade prática e características matemáticas únicas.
Como resultado, a complexa análise matemática desta importante sequência numérica revela surpreendentes padrões educacionais que facilitam a resolução eficiente de problemas matemáticos práticos. Assim sendo, vamos explorar detalhadamente todos os aspectos fundamentais das sequências aritméticas progressivas.
1. Conceitos Matemáticos e Elementos Fundamentais da P.A.
Em primeiro lugar, a estrutura matemática essencial de uma P.A. caracteriza-se pela constante diferença numérica entre seus termos consecutivos calculáveis. Por conseguinte, esta importante regularidade algébrica permite identificar e analisar diversos padrões sequenciais numéricos. Sob o mesmo ponto de vista, um exemplo didático claro aparece na sequência progressiva (2, 5, 8, 11, 14), onde cada número calculado é obtido através da adição sistemática de 3 ao termo anterior.
Além disso, para uma compreensão aprofundada da sequência aritmética, devemos analisar seus elementos matemáticos principais:
- Primeiro termo matemático (a₁): certamente representa o elemento inicial calculável da sequência numérica, funcionando como base fundamental para todos os cálculos progressivos subsequentes
- Razão matemática (r): analogamente define a diferença numérica constante entre termos sequenciais consecutivos, determinando o comportamento progressivo da sequência
- Termo geral algébrico (aₙ): semelhantemente identifica qualquer termo calculável da sequência progressiva, permitindo cálculos precisos em qualquer posição numérica
1.1 Fórmula Matemática do Termo Geral
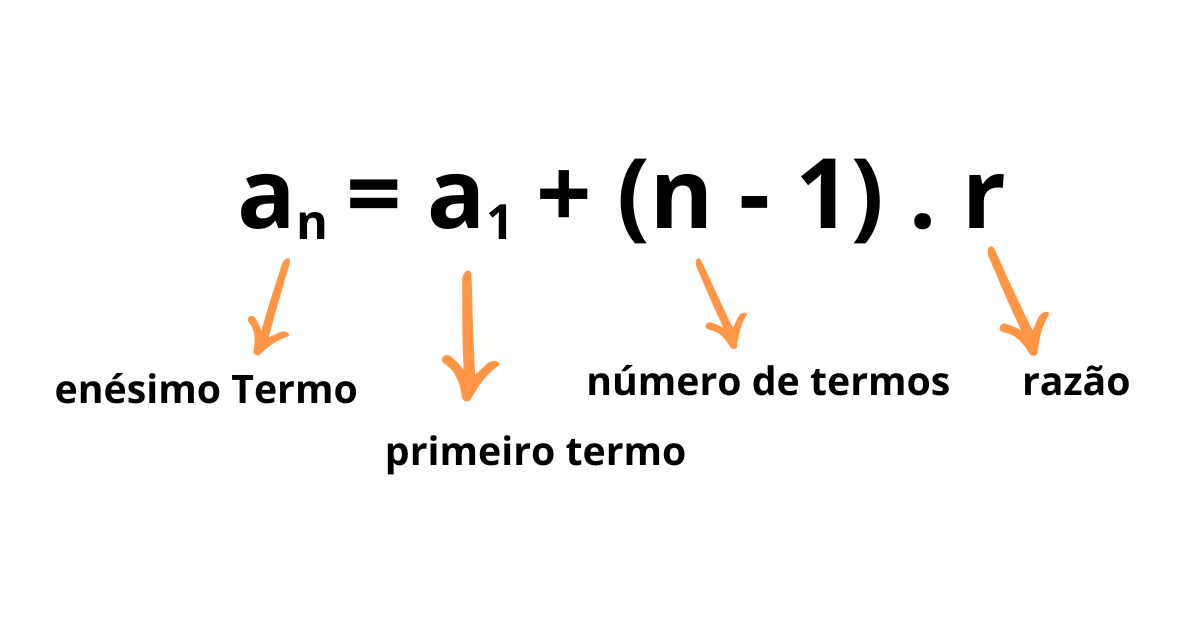
De acordo com a análise, a precisão matemática para encontrar qualquer termo sequencial de uma P.A. utiliza uma fórmula algébrica específica, denominada fórmula calculável do termo geral. Em virtude de, esta expressão matemática pode ser representada como:
Em outras palavras, cada elemento algébrico representa:
- aₙ indica o termo numérico que desejamos calcular na sequência
- a₁ representa o primeiro elemento calculável da sequência progressiva
- n determina a posição numérica do termo procurado na sequência
- r expressa a razão matemática da progressão aritmética
2. Classificação Matemática das P.A.
Sem dúvida, as sequências progressivas aritméticas apresentam diferentes comportamentos matemáticos calculáveis. Por consequência, podemos classificar as P.A.s em três categorias matemáticas distintas:
2.1 P.A. Crescente Progressiva
Nesse sentido, na análise matemática onde a razão é positiva (r > 0), cada termo sequencial calculado supera seu antecessor. Por exemplo, observe o exemplo numérico:
(2, 5, 8, 11, 14), com razão matemática r = 3
Inegavelmente, a sequência progressiva demonstra aumento constante de 3 unidades numéricas entre termos consecutivos.
2.2 P.A. Decrescente Regressiva
Por outro lado, na análise matemática com razão negativa (r < 0), cada termo sequencial calculado é menor que seu antecessor. Logo, analise o exemplo numérico:
(10, 7, 4, 1, -2), com razão matemática r = -3
Em suma, a sequência regressiva apresenta diminuição constante de 3 unidades numéricas entre termos consecutivos.
2.3 P.A. Constante Invariável
Por fim, na análise matemática com razão nula (r = 0), todos os termos sequenciais permanecem idênticos. Em particular, observe o exemplo numérico:
(5, 5, 5, 5, 5), com razão matemática r = 0
Finalmente, a sequência constante mantém valores numéricos inalterados em toda sua extensão.
3. Soma dos Termos de uma P.A.
Certamente, um dos aspectos mais interessantes das progressões aritméticas é o cálculo da soma de seus termos. Com efeito, existe uma fórmula específica que nos permite calcular esta soma de maneira eficiente e elegante.
Primordialmente, para calcular a soma dos n primeiros termos de uma P.A., utilizamos a seguinte fórmula:
Alternativamente, podemos expressar a mesma soma utilizando apenas o primeiro termo e a razão:
Inequivocamente, estas fórmulas são fundamentais para resolver problemas que envolvem somas de sequências aritméticas.
4. Propriedades Importantes da P.A.
Subsequentemente, é crucial compreender algumas propriedades fundamentais das progressões aritméticas:
- Propriedade da média aritmética: em uma P.A., qualquer termo, exceto o primeiro e o último, é igual à média aritmética dos termos vizinhos. Matematicamente: \[ a_n = \frac{a_{n-1} + a_{n+1}}{2} \]
- Propriedade dos termos equidistantes: em uma P.A. finita, a soma de dois termos equidistantes dos extremos é constante e igual à soma do primeiro com o último termo.
- Propriedade da interpolação: ao inserir meios aritméticos entre dois números, todos os números formam uma P.A.
Você vai gostar também:
9 Problemas de Matemática Divertidos para Desafiar sua Mente5. Exercícios Resolvidos e Propostos
Exercício 1:
Determine o 15º termo da P.A. (2, 6, 10, 14, …)
Resolução passo a passo:
- Primeiramente, identificamos os elementos:
- a₁ = 2 (primeiro termo)
- r = 6 – 2 = 4 (razão)
- n = 15 (posição pedida)
- Em seguida, aplicamos a fórmula do termo geral: \[ a_n = a_1 + (n-1)r \] \[ a_{15} = 2 + (15-1)4 \]
- Posteriormente, resolvemos as operações: \[ a_{15} = 2 + (14)4 \] \[ a_{15} = 2 + 56 \] \[ a_{15} = 58 \]
Portanto, o 15º termo da P.A. é 58
Exercício 2:
Em uma P.A., sabe-se que a₁ = 3 e a₁₀ = 30. Determine a razão (r) desta P.A.
Resolução passo a passo:
- Inicialmente, identificamos:
- a₁ = 3
- a₁₀ = 30
- n = 10
- Em seguida, usamos a fórmula do termo geral: \[ a_n = a_1 + (n-1)r \] \[ 30 = 3 + (10-1)r \]
- Posteriormente, resolvemos a equação: \[ 30 = 3 + 9r \] \[ 27 = 9r \] \[ r = 3 \]
Logo, a razão da P.A. é 3
Exercício 3:
A princípio, vamos calcular a soma dos 20 primeiros termos da P.A. (1, 4, 7, …)
Resolução passo a passo:
- Primeiramente, a fim de resolver este exercício, identificamos os elementos:
- Antes de mais nada, temos a₁ = 1
- Em seguida, notamos que r = 4 – 1 = 3
- Por fim, observamos que n = 20
- Posteriormente, com o intuito de avançar na resolução, calculamos o último termo (a₂₀): \[ a_{20} = a_1 + (20-1)r \] \[ a_{20} = 1 + (19)(3) \] \[ a_{20} = 1 + 57 = 58 \]
- Logo após, de acordo com o procedimento, aplicamos a fórmula da soma: \[ S_n = \frac{n(a_1 + a_n)}{2} \] \[ S_{20} = \frac{20(1 + 58)}{2} \] \[ S_{20} = \frac{20(59)}{2} \] \[ S_{20} = 590 \]
Por conseguinte, após todos os cálculos realizados, a soma dos 20 primeiros termos é 590
Exercício 4:
De acordo com o enunciado, em uma progressão aritmética, o primeiro termo é 5 e o último termo é 77. Assim sendo, se esta P.A. tem 20 termos, determine a razão.
Resolução passo a passo:
- Em primeiro lugar, identificamos os dados:
- Primordialmente, temos que a₁ = 5
- Ademais, notamos que a₂₀ = 77
- Além disso, sabemos que n = 20
- Em seguida, com efeito, utilizamos a fórmula do termo geral: \[ a_n = a_1 + (n-1)r \] \[ 77 = 5 + (20-1)r \] \[ 77 = 5 + 19r \]
- De tal forma que, resolvemos a equação: \[ 77 – 5 = 19r \] \[ 72 = 19r \] \[ r = \frac{72}{19} \approx 3,79 \]
Em razão disso, podemos concluir que a razão da P.A. é aproximadamente 3,79
6. Material Complementar e Recursos Adicionais
Sem dúvida, para aprofundar seus conhecimentos sobre progressões aritméticas, recomendamos nosso canal no YouTube. Sendo assim, nesse sentido, você encontrará:
- Sobretudo, videoaulas detalhadas sobre todos os conceitos apresentados
- Da mesma forma, resoluções comentadas de exercícios
- Por outro lado, dicas para provas e concursos
- Por fim, aplicações práticas no dia a dia
De tal sorte que, convidamos você a acessar nosso canal através do link:
Canal MatExpl no YouTubeDicas Essenciais para o Aprendizado
- Precipuamente, pratique regularmente com exercícios variados
- Em contrapartida, identifique os padrões nas sequências
- Analogamente, memorize as fórmulas principais através de sua aplicação
- Em síntese, resolva problemas contextualizados para fixar o conteúdo
Conclusão
Em conclusão, inegavelmente as progressões aritméticas representam um conteúdo fundamental da matemática. Portanto, dominar este tema é essencial para seu desenvolvimento acadêmico e profissional.
Finalmente, de modo que convidamos você a resolver todos os exercícios propostos. Em virtude de todo o exposto, certamente a prática constante é o caminho para a excelência!

Deixe um comentário