A princípio, a trigonometria é um ramo fascinante da matemática que explora as relações entre os lados e os ângulos de um triângulo. No caso específico do triângulo retângulo, surgem três razões trigonométricas que são cruciais para uma infinidade de cálculos e aplicações: o seno, o cosseno e a tangente. Este artigo tem como objetivo guiar você por este mundo, explicando em detalhes o que são essas razões, como calculá-las, e suas aplicações práticas.
Similarmente, nosso objetivo é fornecer um guia completo que sirva como um livro didático, apresentando as razões trigonométricas no triângulo retângulo de forma clara e acessível, ou seja, mesmo para quem está começando a estudar trigonometria agora, poderá compreender este conteúdo.
O que é um triângulo retângulo?
Primeiramente, um triângulo retângulo é definido como um triângulo que possui um ângulo reto, ou seja, um ângulo de exatamente 90°. Além disso, nesses triângulos, é possível identificar alguns elementos:
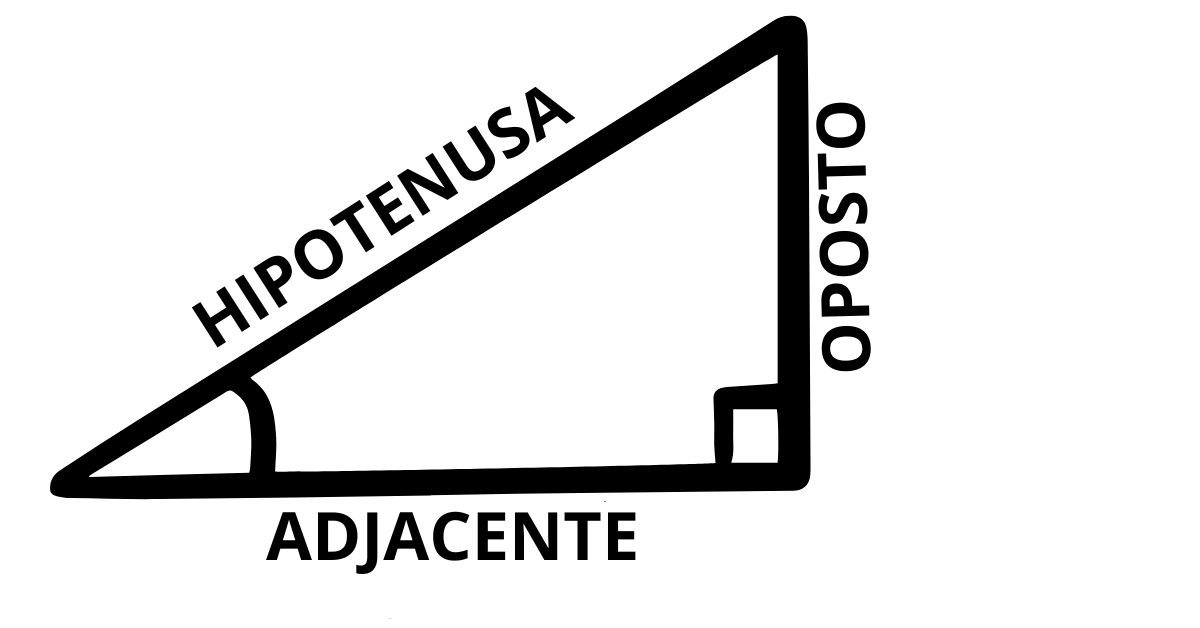
- Hipotenusa: o maior lado do triângulo, sempre oposto ao ângulo reto.
- Catetos: os outros dois lados que formam o ângulo reto.
As Razões Trigonométricas: Seno, Cosseno e Tangente
Para um ângulo agudo θ (diferente do ângulo reto) em um triângulo retângulo, definimos as seguintes razões trigonométricas:
Seno (sen θ) = cateto oposto ÷ hipotenusa
Cosseno (cos θ) = cateto adjacente ÷ hipotenusa
Tangente (tg θ) = cateto oposto ÷ cateto adjacente
Em suma, essas razões trigonométricas estabelecem relações entre as medidas dos lados e os ângulos do triângulo retângulo. Assim sendo, o conhecimento dessas razões, você terá uma base sólida para diversos cálculos trigonométricos.
O estudo das razões trigonométricas no triângulo retângulo é fundamental não apenas para a compreensão da matemática, mas, principalmente, para diversas aplicações no dia a dia, além disso, é um tema recorrente em concursos e vestibulares. Inegavelmente, dominar esses conceitos abrirá portas para muitas outras áreas do saber.
Aplicações Práticas e a Importância nos Estudos
A trigonometria, principalmente as razões trigonométricas no triângulo retângulo, são, por exemplo, ferramentas poderosas com diversas aplicações no mundo real. Por exemplo:
- Engenharia: Engenheiros utilizam as razões trigonométricas para calcular ângulos em construções, estruturas, pontes, etc.
- Navegação: Em sistemas de navegação, é muito útil saber como essas razões funcionam para determinar distâncias, direções e trajetórias.
- Física: A física usa a trigonometria em diversos ramos como, por exemplo, na decomposição de vetores, movimentos, ondas, etc.
- Astronomia: A trigonometria ajuda os astrônomos a determinar distâncias entre estrelas e planetas.
- Topografia: Agrimensores e topógrafos usam essas razões para medir ângulos, distâncias e alturas em terrenos.
- Concursos e Vestibulares: Em provas de concursos e vestibulares, questões que envolvem triângulos retângulos e razões trigonométricas são muito frequentes, principalmente nos certames que envolvem a área da exatas.
Dessa forma, a trigonometria não é apenas um tópico da matemática, mas uma ferramenta para resolução de problemas e compreensão do mundo que nos cerca. Por isso, se você está estudando para concursos e vestibulares, ou até mesmo se é um entusiasta da matemática, esse conteúdo será de grande importância para você.
Tabela com Valores das Razões Trigonométricas de Ângulos Notáveis
Para auxiliar nos seus estudos e na resolução de exercícios, apresento uma tabela com os valores de seno, cosseno e tangente para ângulos comuns:
| Ângulo (θ) | sen θ | cos θ | tan θ |
|---|---|---|---|
| 30° | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{3}}{3}\) |
| 45° | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 |
| 60° | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) |
Exercícios Resolvidos: Passo a Passo
Para solidificar o que aprendemos até aqui, vamos explorar alguns exemplos práticos resolvidos passo a passo:
Exemplo 1
Em um triângulo retângulo, um dos ângulos agudos mede 30°, e a hipotenusa mede 20 cm. Determine o valor do cateto oposto a este ângulo.
Resolução:
1) Usamos a razão seno:
2) \(\sin(30^\circ) = \frac{\text{cateto oposto}}{\text{hipotenusa}}\)
3) Sabemos que \(\sin(30^\circ) = \frac{1}{2}\)
4) \(\frac{1}{2} = \frac{\text{cateto oposto}}{20}\)
5) \(\text{cateto oposto} = 20 \times \frac{1}{2} = 10\) cm
Portanto, o cateto oposto mede 10 cm.
Exemplo 2
Em um triângulo retângulo, o cateto adjacente a um ângulo de 45° mede 12 cm. Determine o valor da hipotenusa.
Resolução:
1) Usamos a razão cosseno:
2) \(\cos(45^\circ) = \frac{\text{cateto adjacente}}{\text{hipotenusa}}\)
3) Sabemos que \(\cos(45^\circ) = \frac{\sqrt{2}}{2}\)
4) \(\frac{\sqrt{2}}{2} = \frac{12}{\text{hipotenusa}}\)
5) \(\text{hipotenusa} = \frac{12}{\frac{\sqrt{2}}{2}} = 12 \times \frac{2}{\sqrt{2}} = \frac{24}{\sqrt{2}}\)
6) Racionalizando, temos que: \(\text{hipotenusa} = 12\sqrt{2}\) cm.
Portanto, o valor da hipotenusa é de \(12\sqrt{2}\) cm.
Exemplo 3
Uma rampa forma um ângulo de 30º com o solo. Se o topo da rampa está a uma altura de 5 metros, qual é o comprimento da rampa?
Resolução:
1) Usamos a razão seno, pois temos o cateto oposto e queremos saber o valor da hipotenusa:
\(\sin(30^\circ) = \frac{\text{cateto oposto}}{\text{hipotenusa}}\)
\(\frac{1}{2} = \frac{5}{\text{hipotenusa}}\)
\(\text{hipotenusa} = \frac{5}{\frac{1}{2}} = 10\) metros
Assim, o comprimento da rampa é de 10 metros.
Exercícios Propostos: Teste Seus Conhecimentos
Agora, chegou a sua vez! Resolva os exercícios abaixo e, em seguida, compare suas respostas com a resolução passo a passo. Lembre-se, o mais importante é tentar e aprender com seus erros!
Questão 1
Um avião decola formando um ângulo de 30° com a horizontal. Se ele percorre uma distância de 10 km no ar, qual a altura que o avião se encontra em relação ao solo?
Questão 2
Uma escada de 6 metros está apoiada em uma parede, formando um ângulo de 60° com o chão. Calcule a distância entre a base da escada e a parede:
Questão 3
Um observador, a uma distância de 20 metros da base de um edifício, vê o topo do edifício sob um ângulo de 45°. Determine a altura do edifício:
Questão 4
O seno de um ângulo agudo é \(\frac{3}{5}\) e a hipotenusa de um triângulo retângulo é 18 cm. Determine o valor do cateto adjacente:
Questão 5
Um triângulo retângulo tem um ângulo de 60°, e o cateto oposto a esse ângulo mede \(12\sqrt{3}\) cm. Quanto mede o cateto adjacente?
Questão 6
Do alto de um farol, que mede 30 metros do nível do mar, um barco é visto sob um ângulo de depressão de 60°. Qual a distância entre o barco e a base do farol?
Questão 7
Um cabo de sustentação de uma torre de transmissão forma um ângulo de 60° com o solo. Sabendo que a torre tem uma altura de 50 metros, qual o comprimento do cabo?
Questão 8
A tangente de um ângulo agudo em um triângulo retângulo é igual a 0.75. Se o cateto adjacente mede 8 cm, quanto mede o cateto oposto?
Se, porventura, você queira explorar mais este tema, não deixe de conferir este vídeo incrível do nosso canal: Vídeos sobre Geometria no Matemática Explorada, onde explicamos em detalhes vários assuntos sobre geometria. Similarmente, você também pode explorar outros assuntos relacionados como distância entre dois pontos aqui no nosso site.
Conclusão
Finalmente, o estudo das razões trigonométricas no triângulo retângulo é, sem dúvida, indispensável para a compreensão da geometria analítica e suas aplicações. Afinal, com o seno, cosseno e tangente, você consegue resolver diversas situações-problema que envolvem triângulos retângulos. Ou seja, o seu aprendizado não deve parar por aqui. Portanto, continue estudando e explorando os fascinantes mistérios da matemática! Compartilhe este artigo com seus amigos e deixe seu comentário abaixo!

Deixe um comentário