Certamente, ao explorar o vasto universo da geometria, nos deparamos com conceitos que, à primeira vista, podem parecer simples, mas que, ao aprofundarmos, revelam uma complexidade fascinante. Um desses conceitos é o de retas perpendiculares. Afinal, o que são retas perpendiculares? Retas perpendiculares são aquelas que se cruzam formando um ângulo reto, ou seja, um ângulo de 90 graus. Este conceito, aparentemente básico, é, em suma, um dos pilares da geometria e está presente, de fato, em inúmeras situações do nosso dia a dia.
Primordialmente, compreender o que são retas perpendiculares e como elas se comportam é essencial para o avanço em outros tópicos da matemática, mas, além disso, é fundamental para a compreensão do mundo que nos rodeia. Em outras palavras, a aplicação deste conceito se estende desde a construção de edifícios até o design de produtos e, por conseguinte, é uma ferramenta indispensável em várias áreas do conhecimento.
A História por Trás das Retas Perpendiculares
Ademais, é relevante ressaltar que a geometria, inclusive o estudo de retas perpendiculares, tem uma longa história. A saber, matemáticos como Euclides, com sua obra “Os Elementos”, já exploravam e formalizavam tais conceitos há mais de dois mil anos. Além disso, os estudos sobre ângulos e retas, e a relação da perpendicularidade, foram sendo refinados ao longo dos séculos por diversos outros matemáticos e, portanto, se tornou um campo essencial para o desenvolvimento da ciência.
Sobretudo, esses estudos nos permitiram entender melhor o mundo que nos cerca e desenvolver tecnologias que utilizamos hoje, tais como a arquitetura e a engenharia. Decerto, a matemática não é apenas um conjunto de fórmulas e cálculos, mas uma forma de ver e compreender o mundo.
O Conceito de Retas Perpendiculares: Uma Visão Detalhada
Primordialmente, retas perpendiculares são aquelas que se encontram formando um ângulo de 90 graus. Aliás, é importante lembrar que o ângulo reto é aquele que corresponde a um quarto de um círculo completo. Similarmente, a perpendicularidade é uma relação geométrica fundamental e, por conseguinte, essencial para a compreensão de outras figuras e relações geométricas.
Assim, para facilitar, vamos definir alguns conceitos importantes:
- Ângulo Reto: Ângulo cuja medida é exatamente 90 graus, frequentemente marcado por um pequeno quadrado no ponto de interseção das retas.
- Interseção: O ponto onde duas ou mais retas se cruzam.
- Perpendicularidade: A relação entre duas retas que se interceptam formando ângulos de 90 graus.
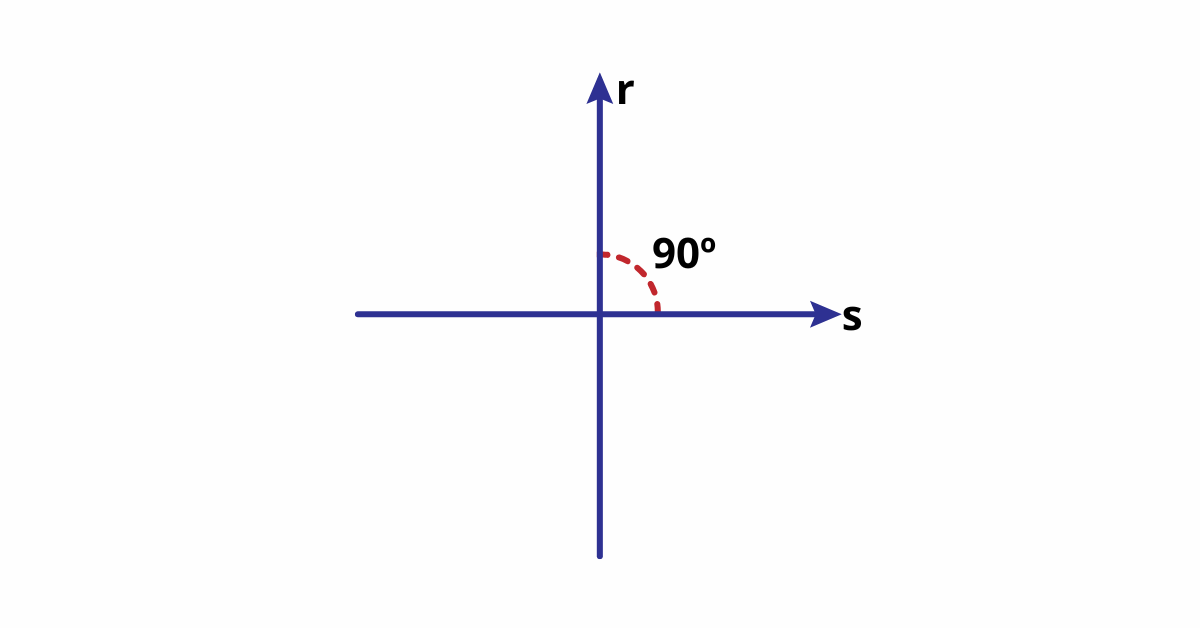
Exemplo de Retas Perpendiculares
Como Identificar Retas Perpendiculares?
A princípio, identificar retas perpendiculares pode parecer desafiador, mas, na prática, é bastante simples. Assim, algumas maneiras de identificar retas perpendiculares são:
- Medição do ângulo: Utilize um transferidor para medir o ângulo formado pela interseção das retas. Se o ângulo for de 90 graus, as retas são perpendiculares.
- Uso de um esquadro: O esquadro possui um ângulo reto e, portanto, pode ser usado para verificar se as retas formam um ângulo de 90 graus.
- Em planos cartesianos: Se as retas estão em um plano cartesiano, e a multiplicação de seus coeficientes angulares resultar em -1, as retas são perpendiculares.
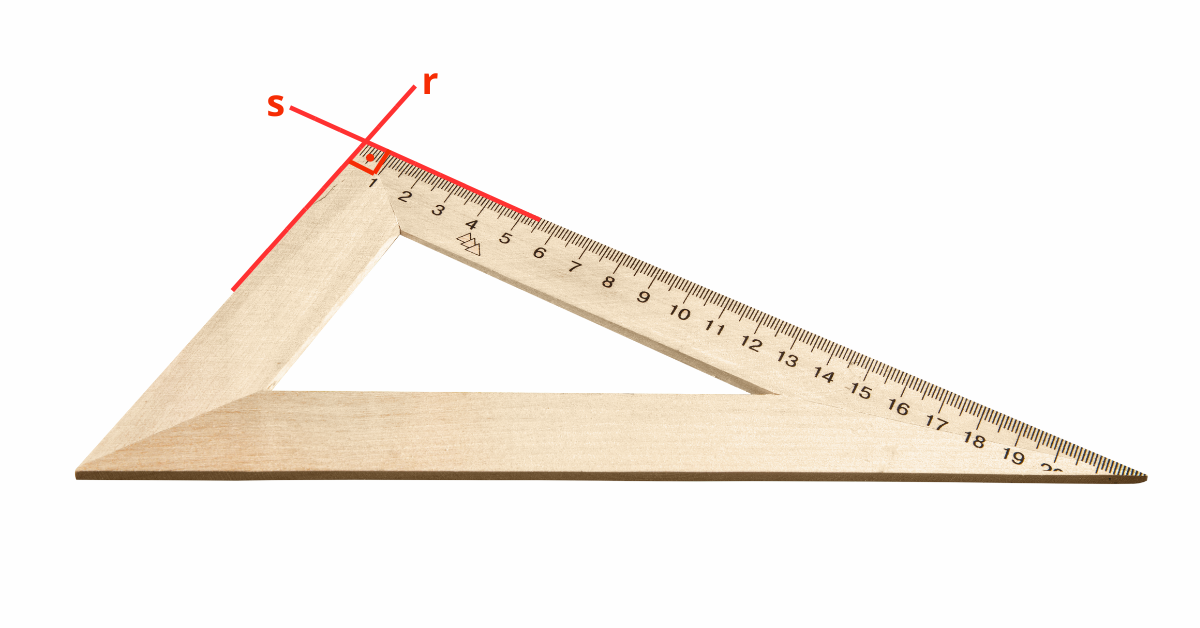
Identificando retas perpendiculares com um esquadro
Retas Perpendiculares no Nosso Dia a Dia: Exemplos Práticos
Inesperadamente, as retas perpendiculares estão ao nosso redor. Diga-se de passagem, observe alguns exemplos:
- Cantos de cômodos: As paredes e o teto do seu quarto, ou qualquer outro cômodo, formam ângulos de 90 graus, o que indica que as retas que formam essas superfícies são perpendiculares.
- Cruzamentos: Em muitas cidades, as ruas se cruzam formando ângulos retos, facilitando a organização do trânsito.
- Ferramentas: Instrumentos como esquadros e réguas utilizam o conceito de retas perpendiculares para garantir a precisão em desenhos e construções.
- Móveis: A maioria dos móveis, como mesas e cadeiras, utiliza ângulos de 90 graus para garantir sua estabilidade e funcionalidade.
- Objetos: Diversos objetos, tais como molduras, janelas, entre outros, são construídos utilizando retas perpendiculares para garantir precisão e simetria.

Retas perpendiculares em edificações
Aplicações da Perpendicularidade em Diversas Áreas
A saber, o conceito de retas perpendiculares é indispensável em várias áreas, tais como:
- Construção Civil: Utilizado para garantir o alinhamento de paredes, pisos e estruturas, além de garantir a segurança em edifícios, pontes e outras construções.
- Design: Essencial na criação de objetos com ângulos precisos, como móveis, ferramentas e embalagens.
- Engenharia: Utilizado no desenho de estruturas, equipamentos e sistemas com precisão e exatidão.
- Cartografia e Navegação: Usado para determinar direções, coordenadas e pontos de referência em mapas e sistemas de navegação.
- Geometria: Fundamental para o estudo de outras formas geométricas, tais como triângulos, quadrados, retângulos, e muito mais.
Como resultado, o conceito de retas perpendiculares é usado em diversas situações cotidianas, além de ser fundamental para diversas áreas profissionais.
Relação da Perpendicularidade e Outros Conceitos Geométricos
Às vezes, a relação entre as retas perpendiculares e outros conceitos geométricos pode não ser tão evidente, mas é importante entendê-la. Por exemplo:
- Retas Paralelas: Retas perpendiculares e paralelas estão interligadas. Quando uma reta intercepta um par de retas paralelas, ela forma ângulos correspondentes iguais.
- Triângulos Retângulos: Um triângulo retângulo, por sua vez, possui um ângulo reto formado por dois lados que são perpendiculares entre si.
- Quadriláteros: Em quadrados e retângulos, todos os lados adjacentes são perpendiculares entre si.
- Planos Perpendiculares: Dois planos são perpendiculares quando o ângulo formado entre suas normais (retas perpendiculares aos planos) é de 90 graus.
Exercícios Resolvidos
A fim de solidificar o que aprendemos até agora, vamos resolver alguns exercícios juntos. Preste bastante atenção e tente entender cada etapa!
Exercício 1
Duas retas, \(r\) e \(s\), se cruzam em um ponto. Se o ângulo formado por elas for de 90 graus, o que podemos afirmar sobre \(r\) e \(s\)?
Resolução:
Se o ângulo formado entre \(r\) e \(s\) é de 90 graus, então, por definição, as retas são perpendiculares.
Portanto, \(r \perp s\)
Exercício 2
Em um plano cartesiano, a reta \(t\) tem coeficiente angular igual a 2. Qual deve ser o coeficiente angular de uma reta \(u\) para que ela seja perpendicular a \(t\)?
Resolução:
Para que duas retas sejam perpendiculares, o produto de seus coeficientes angulares deve ser igual a -1. Seja \(m_t\) o coeficiente angular da reta \(t\) e \(m_u\) o coeficiente angular da reta \(u\). Temos que \(m_t = 2\). Então:
\(m_t \cdot m_u = -1\)
\(2 \cdot m_u = -1\)
\(m_u = – \frac{1}{2}\)
Assim, o coeficiente angular de \(u\) deve ser \(-\frac{1}{2}\).
Exercício 3
Um triângulo tem um ângulo de 90 graus. O que podemos afirmar sobre este triângulo?
Resolução:
Um triângulo com um ângulo de 90 graus é chamado de triângulo retângulo. Os dois lados que formam esse ângulo são perpendiculares entre si.
Exercícios Propostos
Agora, chegou a sua vez! Resolva os exercícios abaixo e, em seguida, compare suas respostas com a resolução passo a passo. Lembre-se, o mais importante é tentar e aprender com seus erros!
Exercício 4
Qual das seguintes afirmações define retas perpendiculares?
Exercício 5
Se uma reta tem inclinação de 30 graus com o eixo x, qual a inclinação de uma reta perpendicular a ela?
Exercício 6
Qual das seguintes formas geométricas sempre possui lados perpendiculares?
Exercício 7
Se duas retas em um plano cartesiano têm coeficientes angulares \(m_1\) e \(m_2\), qual a condição para que elas sejam perpendiculares?
Exercício 8
O ângulo entre as retas que formam um canto de uma parede é de 90 graus. Qual a relação entre essas retas?
Exercício 9
Se um triângulo tem dois lados perpendiculares entre si, qual o tipo desse triângulo?
Se, porventura, você queira explorar mais este tema, não deixe de conferir este vídeo incrível do nosso canal: Vídeos sobre Geometria no Matemática Explorada, onde explicamos em detalhes vários assuntos sobre geometria. Similarmente, você também pode explorar outros assuntos relacionados como retas paralelas e transversais aqui: Retas Paralelas e Transversais.
Conclusão
Enfim, o estudo das retas perpendiculares é fundamental não apenas para o avanço na matemática, mas também para a compreensão do mundo ao nosso redor. Por isso, ao dominar este conceito, você estará apto para desvendar as inúmeras aplicações geométricas, e, além disso, desenvolver habilidades de raciocínio lógico e resolução de problemas. Apesar disso, a jornada do aprendizado não termina aqui. Portanto, continue explorando os fascinantes segredos da matemática em nosso site.

Deixe um comentário