Matemática Explorada

Primordialmente, após explorarmos a introdução e as formas de representação das funções em artigos anteriores (Funções Matemáticas: Introdução e Representar Funções: Notação, Diagramas e Gráficos), agora, vamos adentrar no universo dos tipos de funções, começando pelas funções lineares e afins. Assim sendo, este artigo tem o propósito de desvendar o que são, como funcionam e onde encontramos essas funções no nosso dia a dia.

Sobretudo, entender os diferentes tipos de funções é fundamental para modelar e analisar uma ampla gama de situações. Inegavelmente, as funções lineares e afins são as mais básicas e comuns, servindo como base para outros tipos mais complexos. Então, prepare-se para embarcar nesta jornada de aprendizado e descobrir o poder das funções lineares e afins!

Funções Lineares: Uma Reta que Passa pela Origem

A princípio, uma função linear é aquela que pode ser expressa na forma \( f(x) = ax \), onde \( a \) é um número real conhecido como coeficiente angular. Analogamente, o gráfico de uma função linear é sempre uma reta que passa pela origem do plano cartesiano (ponto (0,0)). Aliás, essa característica faz com que a função linear seja diretamente proporcional, ou seja, quando x aumenta, f(x) aumenta na mesma proporção.

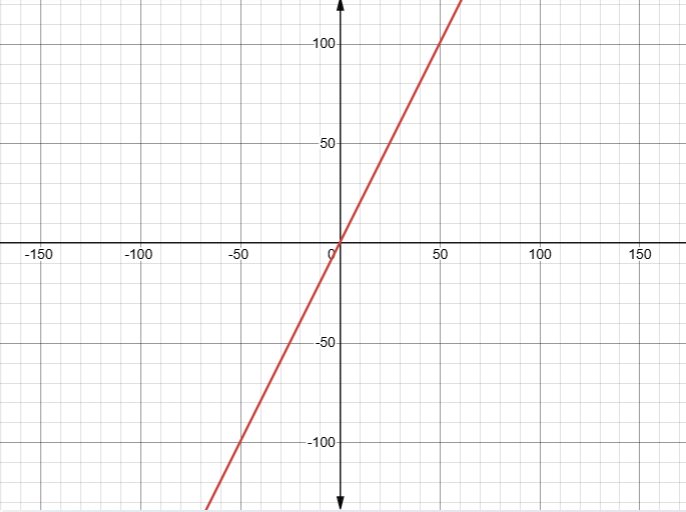
Em outras palavras, o coeficiente angular \( a \) determina a inclinação da reta. A saber, se \( a \) for positivo, a reta será crescente (subirá da esquerda para a direita); se \( a \) for negativo, a reta será decrescente (descerá da esquerda para a direita). Portanto, o valor de \( a \) define o comportamento da função linear.

Funções Afins: Uma Reta que Pode Não Passar pela Origem

Antes de mais nada, uma função afim é uma generalização da função linear, sendo expressa na forma \( f(x) = ax + b \), onde \( a \) e \( b \) são números reais. Nesse sentido, \( a \) continua sendo o coeficiente angular, e \( b \) é conhecido como coeficiente linear ou termo independente. Assim, o gráfico de uma função afim é uma reta que não necessariamente passa pela origem.

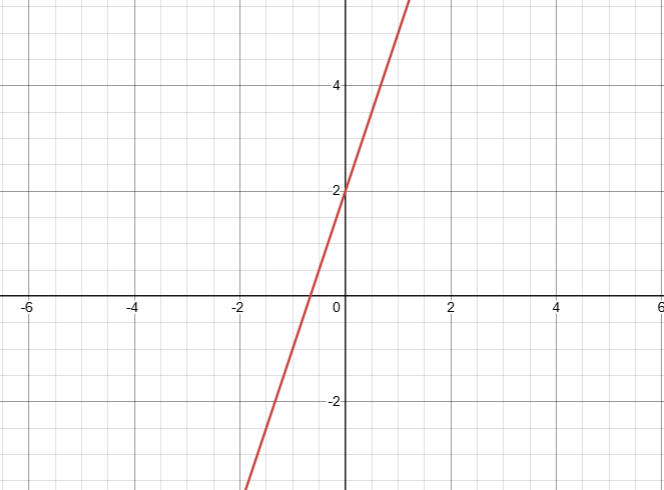
Em resumo, o coeficiente angular \( a \) ainda determina a inclinação da reta, enquanto o coeficiente linear \( b \) define o ponto onde a reta corta o eixo y. Dessa forma, as funções afins representam uma classe mais ampla de relações lineares, que podem modelar muitas situações reais.

Entendendo os Coeficientes

Em primeiro lugar, é fundamental compreender o papel dos coeficientes \( a \) e \( b \). A saber, o coeficiente angular \( a \) indica a taxa de variação da função. Isto é, ele mostra o quanto \( f(x) \) muda quando \( x \) aumenta uma unidade. Por exemplo, em uma função \( f(x) = 2x \), cada aumento de 1 em \( x \) causa um aumento de 2 em \( f(x) \).

Por outro lado, o coeficiente linear \( b \) indica o valor de \( f(x) \) quando \( x \) é zero. Em outras palavras, ele define o ponto onde a reta intercepta o eixo y. Assim também, na função \( f(x) = 3x + 2 \), a reta intercepta o eixo y no ponto (0, 2). Dessa maneira, os coeficientes \( a \) e \( b \) nos dão informações cruciais sobre o comportamento da função.

Exemplos Práticos de Funções Lineares e Afins

De fato, as funções lineares e afins aparecem em inúmeras situações do nosso dia a dia. Por exemplo, a relação entre o tempo e a distância percorrida por um carro a uma velocidade constante pode ser modelada por uma função linear. A saber, se um carro viaja a 60 km/h, a função \( d(t) = 60t \) (onde d é a distância e t é o tempo) descreve essa relação.

Similarmente, uma função afim pode modelar um custo fixo mais um custo variável. Por exemplo, o custo total de uma corrida de táxi pode ser expresso como \( C(x) = 2x + 5 \), onde \( x \) é a distância percorrida em km, 2 é o custo por km e 5 é a taxa fixa da corrida. Assim, as funções lineares e afins nos ajudam a entender e prever situações cotidianas.

Identificando Funções Lineares e Afins a Partir de Gráficos

Eventualmente, a análise de um gráfico permite identificar se uma função é linear ou afim. Nesse sentido, se o gráfico for uma reta que passa pela origem, a função é linear. Logo, se o gráfico for uma reta que não passa necessariamente pela origem, a função é afim. Outrossim, a inclinação da reta nos dá o valor do coeficiente angular \( a \).

Além disso, a intersecção da reta com o eixo y nos fornece o valor do coeficiente linear \( b \) em uma função afim. Portanto, a análise gráfica é uma ferramenta muito útil para entender o comportamento dessas funções.

Como Construir Funções Lineares e Afins a Partir de Pares Ordenados

Certamente, podemos construir funções lineares e afins a partir de pares ordenados. Em resumo, se tivermos dois pontos distintos (x1, y1) e (x2, y2), podemos encontrar a função afim \( f(x) = ax + b \) que passa por esses pontos. Assim, para isso, calculamos o coeficiente angular \( a \) usando a fórmula:

Posteriormente, com o valor de \( a \) e um dos pontos, podemos substituir na equação \( y = ax + b \) e encontrar o valor de \( b \). Assim sendo, o conhecimento de pares ordenados nos permite determinar a expressão algébrica da função.

Funções Lineares e Afins na História da Matemática

Antes de tudo, as funções lineares e afins têm uma longa história na matemática. Principalmente, os gregos antigos já estudavam relações lineares na geometria. Entretanto, foi com o desenvolvimento do cálculo que as funções lineares e afins ganharam uma importância central. Inegavelmente, matemáticos como René Descartes e Isaac Newton contribuíram para formalizar esses conceitos.

Conforme avançava o estudo da matemática, as funções lineares e afins se mostraram ferramentas essenciais para modelar e entender o mundo ao nosso redor. De fato, desde a física até a economia, essas funções são a base para muitas outras áreas do conhecimento.

Importância e Conexão com Próximos Artigos

Em conclusão, as funções lineares e afins são conceitos fundamentais na matemática, servindo como base para muitos outros conceitos mais avançados. Acima de tudo, entender suas propriedades e aplicações é essencial para prosseguir no estudo de funções e outras áreas da matemática. Todavia, esta é apenas mais uma etapa em nossa jornada de descoberta.

Nesse sentido, nos próximos artigos, exploraremos outros tipos de funções, como quadráticas, exponenciais e logarítmicas, bem como nos aprofundaremos na representação gráfica e nas aplicações das funções no dia a dia. Assim, convido você a continuar sua jornada de aprendizado e aprofundar seus conhecimentos!

Para complementar seus estudos, você pode conferir nossos artigos sobre Funções Matemáticas: Introdução e Representar Funções: Notação, Diagramas e Gráficos, onde você poderá explorar mais sobre o tema!

Não perca a oportunidade de aprender mais! Inscreva-se agora em nosso canal no YouTube e descubra vídeos incríveis sobre matemática: Matemática Explorada. **Junte-se à nossa comunidade e vamos desvendar os mistérios da matemática juntos!**

Exercícios Propostos