Transformações de Funções: Guia Completo e Prático

Transformações de Funções: Um Guia Completo e Prático

Olá, estudante! Depois de explorar diversas famílias de funções (quadráticas, exponenciais, trigonométricas, etc), é hora de um novo desafio: as transformações de funções. Nesse sentido, as transformações nos permitem manipular funções, alterando seus gráficos e equações de maneira precisa e controlada. Neste artigo, portanto, vamos explorar os diferentes tipos de transformações e como elas podem ser aplicadas.

Introdução às Transformações de Funções

Em resumo, as transformações de funções são operações que alteram o gráfico de uma função, mudando sua forma, posição ou tamanho. A saber, essas operações são realizadas diretamente na equação da função, resultando em novas funções com características distintas. Ainda assim, as transformações são essenciais para entender a relação entre a equação e o gráfico de uma função.

Principalmente, existem quatro tipos básicos de transformações:

Translação: Desloca o gráfico horizontalmente ou verticalmente.
Reflexão: Espelha o gráfico em relação a um eixo.
Dilatação: Estira o gráfico vertical ou horizontalmente.
Compressão: Encolhe o gráfico vertical ou horizontalmente.

Por exemplo, uma transformação pode mover o gráfico de uma função quadrática para cima, para a direita ou espelhá-lo em relação a um eixo. Certamente, compreender essas transformações nos permite criar novas funções a partir de funções conhecidas.

Translações de Funções

Primordialmente, as translações são transformações que deslocam o gráfico de uma função sem alterar sua forma. Em outras palavras, essas translações podem ser verticais (para cima ou para baixo) ou horizontais (para a direita ou para a esquerda).

Translação Vertical

Uma translação vertical desloca o gráfico para cima ou para baixo. Para transladar o gráfico de uma função \(f(x)\) verticalmente por \(k\) unidades, adicionamos ou subtraímos \(k\) da função.

Se \(k > 0\): O gráfico é deslocado \(k\) unidades para cima: \(g(x) = f(x) + k\).
Se \(k < 0\): O gráfico é deslocado \(-k\) unidades para baixo: \(g(x) = f(x) - k\).

Translação Horizontal

Analogamente, uma translação horizontal desloca o gráfico para a direita ou para a esquerda. Para transladar o gráfico de uma função \(f(x)\) horizontalmente por \(h\) unidades, adicionamos ou subtraímos \(h\) do argumento da função.

Se \(h > 0\): O gráfico é deslocado \(h\) unidades para a esquerda: \(g(x) = f(x + h)\).
Se \(h < 0\): O gráfico é deslocado \(-h\) unidades para a direita: \(g(x) = f(x - h)\).

Por exemplo, a função \(f(x) = x^2 + 2\) é uma translação vertical de 2 unidades para cima da função \(f(x) = x^2\). Similarmente, a função \(f(x) = (x – 3)^2\) é uma translação horizontal de 3 unidades para a direita da função \(f(x) = x^2\).

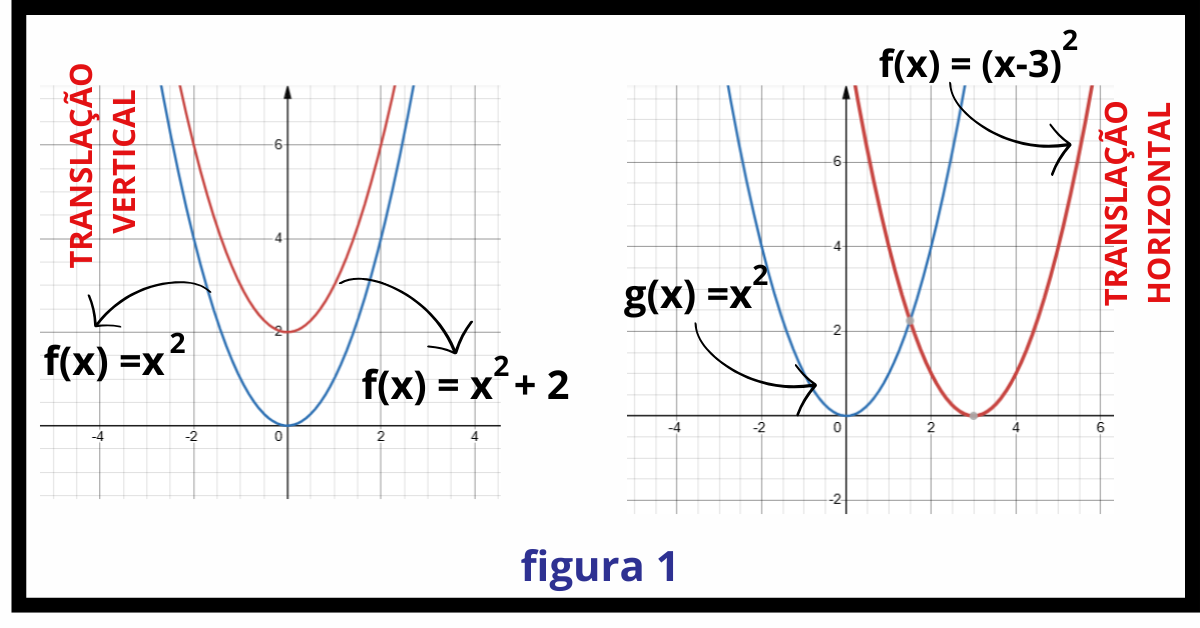
Figura 1: Translações horizontal e vertical de uma função.

Reflexões de Funções

Em contrapartida, as reflexões espelham o gráfico de uma função em relação a um eixo, ou seja, o eixo x ou o eixo y. Assim sendo, essas transformações também afetam a equação da função de forma específica.

Reflexão em Relação ao Eixo x

Uma reflexão em relação ao eixo x inverte o gráfico verticalmente. Para refletir o gráfico de uma função \(f(x)\) em relação ao eixo x, multiplicamos a função por -1.

\[ g(x) = -f(x) \]

Reflexão em Relação ao Eixo y

Analogamente, uma reflexão em relação ao eixo y inverte o gráfico horizontalmente. Para refletir o gráfico de uma função \(f(x)\) em relação ao eixo y, substituímos \(x\) por \(-x\).

\[ g(x) = f(-x) \]

Por exemplo, a função \(g(x) = -x^2\) é uma reflexão da função \(f(x) = x^2\) em relação ao eixo x. Do mesmo modo, a função \(g(x) = \sqrt{-x}\) é uma reflexão da função \(f(x) = \sqrt{x}\) em relação ao eixo y.

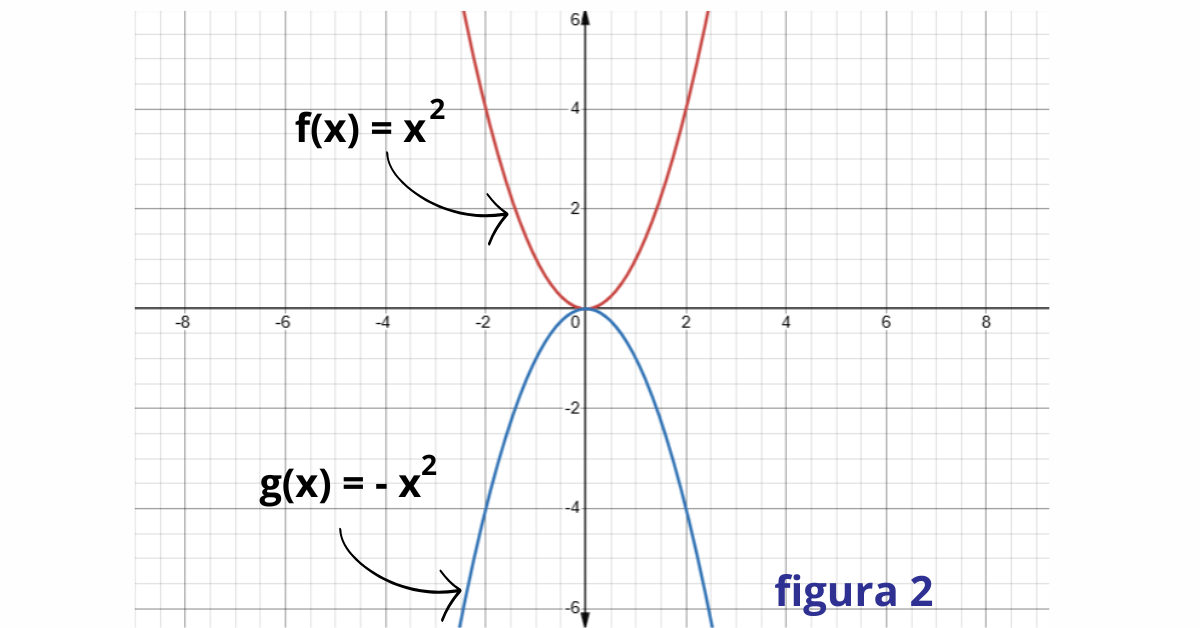
Figura 2: Reflexão de uma função em relação aos eixos x e y.

Dilatações e Compressões de Funções

As dilatações e compressões esticam ou encolhem o gráfico de uma função. Contudo, essas transformações podem ser verticais ou horizontais.

Dilatação e Compressão Vertical

Uma dilatação vertical estica o gráfico verticalmente, enquanto uma compressão vertical o encolhe nessa mesma direção. Para dilatar ou comprimir o gráfico de uma função \(f(x)\) verticalmente por um fator \(a\), multiplicamos a função por \(a\).

Se \( a > 1 \): O gráfico é esticado verticalmente (dilatação).
Se \( 0 < a < 1 \): O gráfico é encolhido verticalmente (compressão).

\[ g(x) = a \cdot f(x) \]

Dilatação e Compressão Horizontal

Similarmente, uma dilatação horizontal estica o gráfico horizontalmente, enquanto uma compressão horizontal o encolhe nessa direção. Para dilatar ou comprimir o gráfico de uma função \(f(x)\) horizontalmente por um fator \(b\), multiplicamos o argumento da função por \(b\).

Se \( b > 1 \): O gráfico é encolhido horizontalmente (compressão).
Se \( 0 < b < 1 \): O gráfico é esticado horizontalmente (dilatação).

\[ g(x) = f(b \cdot x) \]

Por exemplo, a função \(g(x) = 2x^2\) é uma dilatação vertical da função \(f(x) = x^2\), e a função \(g(x) = \left(\frac{1}{2}x\right)^2\) é uma dilatação horizontal da função \(f(x) = x^2\).

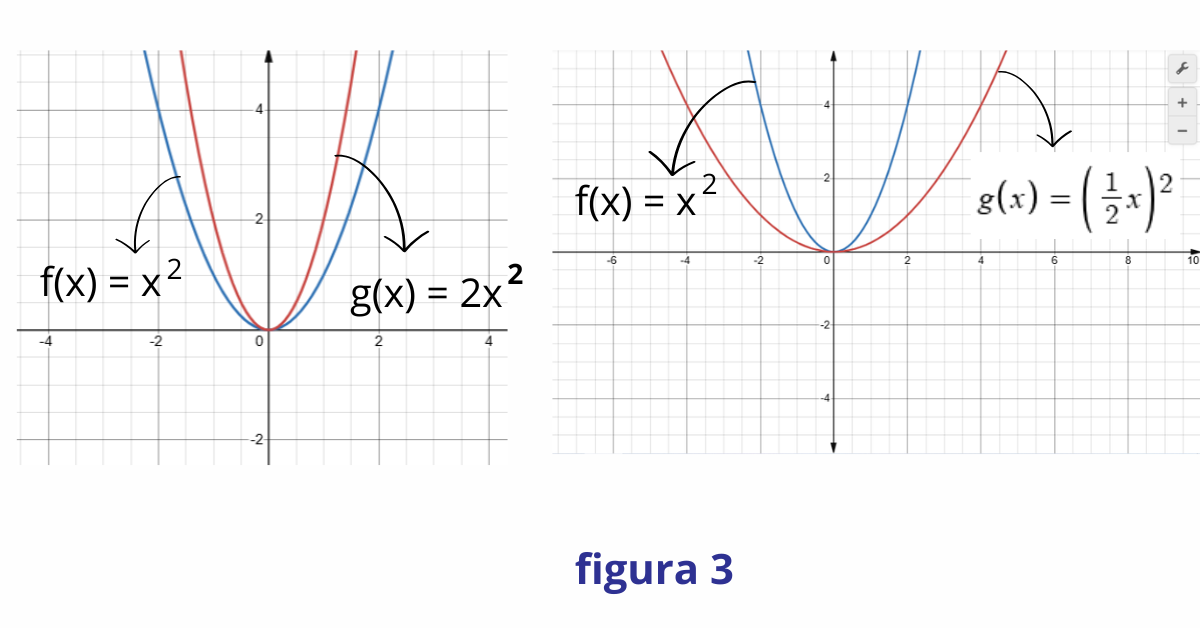
Figura 3: Dilatações vertical e horizontal de uma função.

Combinação de Transformações

As transformações, ainda mais, podem ser combinadas para gerar funções ainda mais complexas. A fim de aplicar múltiplas transformações, é preciso seguir uma ordem específica, geralmente:

Dilatações e Compressões
Reflexões
Translações

Por exemplo, para transformar a função \(f(x) = x^2\) em \(g(x) = -2(x-3)^2 + 4\), primeiro, realizamos uma dilatação vertical por 2, depois uma reflexão em relação ao eixo x, em seguida uma translação horizontal de 3 unidades para a direita e, por último, uma translação vertical de 4 unidades para cima.

Aplicações das Transformações de Funções

As transformações de funções, eventualmente, encontram diversas aplicações em áreas como física, engenharia, design gráfico, processamento de sinais, entre outros. Isto é, elas são ferramentas valiosas para modelagem e análise de dados.

Um Pouco de História

O estudo das transformações de funções, por outro lado, não possui uma história tão direta como o desenvolvimento de outros conceitos matemáticos. No entanto, o conceito de funções e seus gráficos se desenvolveu ao longo do tempo com o trabalho de muitos matemáticos, como René Descartes, que introduziu o sistema de coordenadas cartesianas. Contudo, a manipulação de gráficos e funções se tornou mais precisa com o desenvolvimento do cálculo e suas aplicações.

Exercícios Propostos

Agora, chegou a sua vez! Resolva os exercícios abaixo e, em seguida, compare suas respostas com a resolução passo a passo. Lembre-se, o mais importante é tentar e aprender com seus erros!

Exercício 1

Qual transformação desloca o gráfico de \(f(x)\) para cima?

A) \(f(x + k)\) com \(k > 0\)
B) \(f(x) + k\) com \(k > 0\)
C) \(f(-x)\)
D) \(-f(x)\)

Exercício 2

Qual transformação reflete o gráfico de \(f(x)\) em relação ao eixo x?

A) \(f(x + k)\)
B) \(f(x) – k\)
C) \(-f(x)\)
D) \(f(-x)\)

Exercício 3

Qual transformação estica o gráfico de \(f(x)\) horizontalmente?

A) \(a \cdot f(x)\) com \(a > 1\)
B) \(f(b \cdot x)\) com \(b > 1\)
C) \(f(b \cdot x)\) com \(0 < b < 1\)
D) \(f(x + h)\)

Exercício 4

Se \(f(x) = x^2\), qual a função após translação vertical de 3 unidades para cima?

A) \(f(x) = (x + 3)^2\)
B) \(f(x) = (x – 3)^2\)
C) \(f(x) = x^2 + 3\)
D) \(f(x) = x^2 – 3\)

Exercício 5

Se \(f(x) = \sqrt{x}\), qual a função após reflexão em relação ao eixo y?

A) \(f(x) = -\sqrt{x}\)
B) \(f(x) = \sqrt{-x}\)
C) \(f(x) = \sqrt{x} + k\)
D) \(f(x) = \sqrt{x} – k\)

Exercício 6

Se \(f(x) = \sin(x)\), qual a função após dilatação vertical por um fator de 2?

A) \(f(x) = \frac{1}{2}\sin(x)\)
B) \(f(x) = \sin(2x)\)
C) \(f(x) = 2\sin(x)\)
D) \(f(x) = \sin(\frac{1}{2}x)\)

Exercício 7

Se \(f(x) = x^3\), qual a função após uma translação horizontal de 2 unidades para a direita e uma reflexão em relação ao eixo x?

A) \(f(x) = -(x + 2)^3\)
B) \(f(x) = (x – 2)^3\)
C) \(f(x) = -(x – 2)^3\)
D) \(f(x) = -(x + 2)^3\)

Exercício 8

A função \( g(x) = \frac{1}{2}(x+1)^2 – 3\), qual transformação não foi utilizada?

A) translação vertical
B) dilatação horizontal
C) compressão vertical
D) translação horizontal

Para complementar seus estudos, confira nosso artigo anterior sobre funções quadráticas. Além disso, explore nosso canal no YouTube Matemática Explorada, onde você encontrará mais conteúdos didáticos e interessantes!

Conclusão

Em conclusão, as transformações de funções são ferramentas poderosas para manipular gráficos e equações. Por meio das translações, reflexões e dilatações, enfim, podemos gerar novas funções a partir de funções conhecidas. Logo, o estudo dessas transformações amplia nosso entendimento sobre o comportamento das funções e suas aplicações. Acima de tudo, continue praticando e explorando os conceitos e aplicações.