**Transformações Geométricas**, um conceito central na geometria, referem-se a operações que alteram a posição, tamanho ou forma de uma figura geométrica no plano ou no espaço. **Primeiramente**, vamos explorar as principais transformações e entender como elas funcionam. **Ademais**, este artigo irá guiá-lo através dos conceitos fundamentais, fornecendo exemplos práticos e exercícios para consolidar seu aprendizado.
O Que São Transformações Geométricas?
**A princípio**, é importante entender que transformações geométricas são operações que pegam uma figura inicial (chamada de pré-imagem) e a convertem em uma nova figura (chamada de imagem). **Analogamente**, pense em um espelho: ele reflete uma imagem, mas a imagem não é idêntica à pessoa que está na frente do espelho. **Aliás**, essas transformações podem envolver movimentos como rotações, reflexões e translações, **bem como** alterações de tamanho como as ampliações e reduções.
Tipos Principais de Transformações Geométricas
**Atualmente**, as transformações geométricas são classificadas em isométricas (que preservam as medidas) e não isométricas (que alteram as medidas). **Em primeiro lugar**, vamos conhecer as principais.
Translação
**De fato**, a translação é um movimento que desloca cada ponto de uma figura na mesma direção e com a mesma distância. **Em outras palavras**, é como deslizar uma figura sem girá-la ou deformá-la.
**Só para exemplificar**, imagine que você tem um triângulo desenhado em um papel. Se você pegar esse triângulo e movê-lo para a direita e para cima sem girá-lo, você estará realizando uma translação.
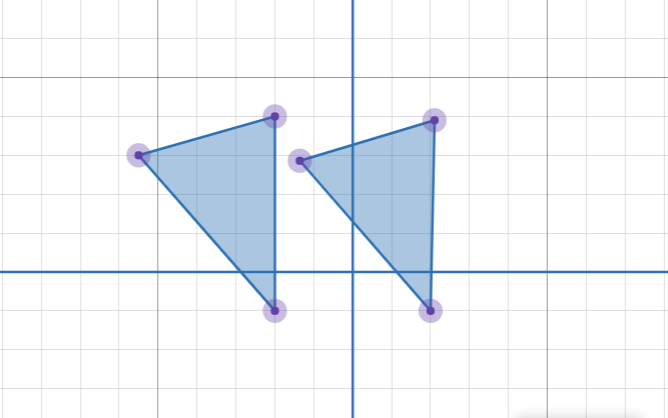
Rotação
**Por outro lado**, a rotação consiste em girar uma figura em torno de um ponto fixo (centro de rotação) por um determinado ângulo.
**A saber**, pense em um ventilador: as pás giram em torno de um ponto central. Da mesma forma, na rotação geométrica, todos os pontos da figura são girados no mesmo ângulo em torno de um ponto fixo.
Reflexão
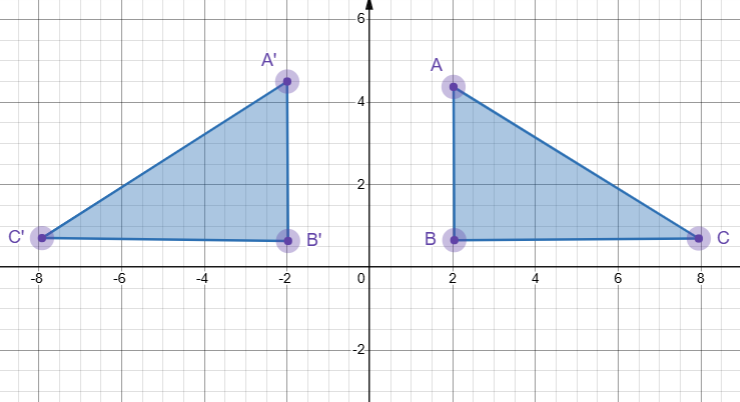
**Nesse sentido**, a reflexão é como um espelho: cria uma imagem simétrica de uma figura em relação a uma reta (eixo de reflexão).
**Por exemplo**, se você colocar um triângulo em frente a um espelho, a imagem refletida será uma reflexão do triângulo.
Homotetia
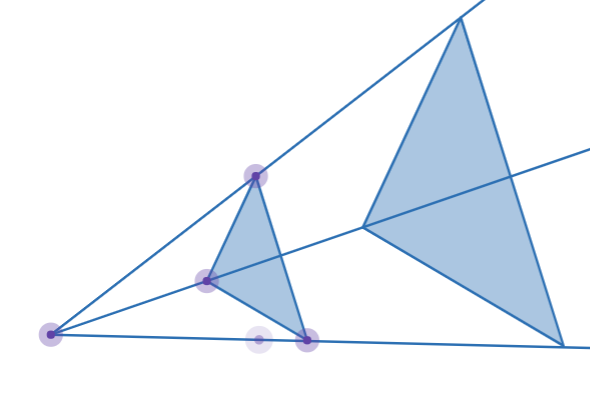
**Além disso**, a homotetia é uma transformação que amplia ou reduz uma figura a partir de um ponto fixo (centro de homotetia).
**Só para ilustrar**, imagine que você está usando uma lupa. Se você aumentar a lupa, os objetos parecerão maiores, e se você diminuir a lupa, os objetos parecerão menores. Isso é semelhante à homotetia na geometria.
Matemáticos e a História das Transformações Geométricas
**Certamente**, o estudo das transformações geométricas tem raízes antigas. **Antes de tudo**, os gregos já exploravam conceitos como simetria e isometria. **Entretanto**, foi no século XIX, com o desenvolvimento da geometria projetiva e da álgebra linear, que essas transformações ganharam uma base matemática mais sólida. **Principalmente**, matemáticos como Felix Klein e Arthur Cayley fizeram importantes contribuições:
Felix Klein (1849-1925) foi um matemático alemão que propôs o “Programa de Erlangen”, que utilizava a teoria de grupos para classificar as geometrias com base em suas transformações invariantes. As transformações geométricas desempenham um papel central nesse programa, ajudando a entender diferentes tipos de geometrias.
Arthur Cayley (1821-1895), um matemático britânico, fez contribuições importantes para a álgebra linear, que é essencial para o estudo das transformações geométricas. Suas pesquisas sobre matrizes e transformações lineares influenciaram profundamente a forma como entendemos essas transformações hoje.
Aplicações Práticas das Transformações Geométricas
**Logo**, as transformações geométricas não são apenas conceitos abstratos. **Em resumo**, elas são amplamente utilizadas em diversas áreas:
- Gráficos por computador: **Inegavelmente**, a criação de jogos, filmes e animações depende fortemente das transformações geométricas para mover, rotacionar e escalar objetos. Por exemplo, em um jogo 3D, personagens e objetos são movimentados, rotacionados e redimensionados usando transformações geométricas.
- Design e arquitetura: **Da mesma forma**, elas são utilizadas para criar padrões, estruturas e simulações de projetos. Na arquitetura, as transformações geométricas são essenciais para planejar a planta de um edifício ou para gerar padrões repetitivos em fachadas e interiores.
- Engenharia: **Assim também**, o estudo de estruturas e o movimento de peças mecânicas se beneficiam das transformações geométricas. Os engenheiros usam transformações geométricas para modelar e analisar o comportamento de estruturas, como pontes e edifícios.
- Medicina: **De fato**, as imagens médicas como ressonâncias magnéticas e tomografias são processadas utilizando transformações geométricas para corrigir distorções, alinhar diferentes imagens ou criar modelos tridimensionais.
Exercícios
1. Qual das seguintes transformações geométricas preserva as medidas de ângulos e distâncias?
- Homotetia
- Reflexão
- Translação
- Rotação
- Todas as alternativas, exceto a letra “a”
Resposta: A alternativa correta é a letra “e”.
Resolução: A homotetia altera o tamanho da figura, enquanto as demais transformações preservam as medidas. As transformações que preservam as medidas são conhecidas como isometrias. São elas: reflexão, translação e rotação.
2. Uma figura é refletida em relação a um eixo e, em seguida, transladada. Qual o efeito dessas transformações?
- A figura mantém a mesma orientação e posição
- A figura é invertida e deslocada
- A figura permanece na mesma posição, mas com tamanho alterado
- A figura é rotacionada
- Nenhuma das anteriores
Resposta: A alternativa correta é a letra “b”.
Resolução: A reflexão inverte a figura, e a translação desloca-a para uma nova posição. Portanto, a figura é invertida e deslocada.
3. Se um triângulo equilátero é rotacionado em 60° graus em torno de um de seus vértices, qual será a nova forma resultante?
- Um triângulo retângulo
- Um triângulo isósceles
- Um triângulo semelhante ao inicial
- Um losango
- Um hexágono
Resposta: A alternativa correta é a letra “c”.
Resolução: A rotação preserva a forma e as medidas do triângulo, portanto, a nova figura será um triângulo equilátero, que é semelhante ao inicial.
4. Um quadrado de lado 2 cm é submetido a uma homotetia de razão 3 a partir do centro. Qual será o lado do novo quadrado?
- 2 cm
- 3 cm
- 4 cm
- 6 cm
- 8 cm
Resposta: A alternativa correta é a letra “d”.
Resolução: Em uma homotetia, as medidas da figura são multiplicadas pela razão da homotetia. Portanto, o novo lado será 2 cm * 3 = 6 cm.
5. Um ponto de coordenadas (3, -2) é transladado pelo vetor (-1, 4). Quais serão as coordenadas do ponto resultante após a translação?
- (4, 2)
- (2, 2)
- (4, -6)
- (2, -6)
- (3, -2)
Resposta: A alternativa correta é a letra “b”.
Resolução: A translação de um ponto é obtida somando as coordenadas do vetor de translação às coordenadas do ponto original. Então, (3 – 1, -2 + 4) = (2, 2).
6. Um triângulo ABC com vértices A(1,1), B(3,1) e C(1,3) é refletido em relação ao eixo x. Quais as coordenadas dos vértices do triângulo refletido?
- A'(1,-1), B'(3,-1), C'(1, -3)
- A'(-1,1), B'(-3,1), C'(-1, 3)
- A'(1,1), B'(3,1), C'(1, 3)
- A'(-1,-1), B'(-3,-1), C'(-1, -3)
- A'(1,-1), B'(3,-1), C'(3, -1)
Resposta: A alternativa correta é a letra “a”.
Resolução: Ao refletir em relação ao eixo x, a coordenada y de cada ponto é multiplicada por -1. Assim, A’ = (1, -1), B’ = (3, -1) e C’ = (1, -3).
**Em suma**, as transformações geométricas são ferramentas poderosas na matemática e em muitas outras áreas. **Portanto**, esperamos que este artigo tenha elucidado os principais conceitos e instigado seu interesse por este fascinante campo de estudo.
Para complementar seus estudos, você pode conferir nosso artigo sobre Retas Perpendiculares, onde você poderá explorar mais sobre geometria!
**Não perca a oportunidade de aprender mais!** Inscreva-se agora em nosso canal no YouTube e descubra vídeos incríveis sobre matemática: Matexpl
Este artigo foi desenvolvido com o objetivo de oferecer uma visão geral das transformações geométricas, combinando teoria, exemplos práticos e aplicações relevantes. Esperamos que tenha sido útil e inspirador.

Deixe um comentário